Шағын топтардың торы - Википедия - Lattice of subgroups
Жылы математика, кіші топтардың торы а топ болып табылады тор оның элементтері кіші топтар туралы , бірге ішінара тапсырыс қатынас болу қосу.Бұл торда екі топшаның қосылысы ішкі топ болып табылады құрылған олардың одақ, және екі кіші топтың кездесуі олардың қиылысу.
Мысал
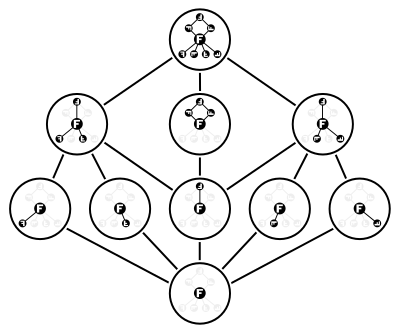
The екіжақты топ Дих4 өзін және the-ді есептейтін он топшасы бар тривиалды кіші топ. Сегіз топтық элементтердің бесеуі екінші ретті ішкі топтарды құрайды, ал қалған екі жеке емес элементтер де бірдей жасайды циклдік төртінші тапсырыстың кіші тобы. Сонымен қатар, форманың екі топшасы бар З2 × Z2, ретті-екі элементтің жұптары тудырады. Осы он топшадан құралған тор суретте көрсетілген.
Бұл мысал топтың барлық кіші топтарының торы а емес екенін көрсетеді модульдік тор жалпы алғанда. Шынында да, дәл осы торда тыйым салынған «бесбұрыш» бар N5 сияқты субтитр.
Қасиеттері
Кез келген үшін A, B, және C топтың кіші топтары A ≤ C (A кіші тобы C) содан кейін AB ∩ C = A (B ∩ C); мұндағы көбейту кіші топтардың өнімі. Бұл қасиет деп аталады топтардың модульдік қасиеті (Ашбахер 2000 ) немесе (Dedekind модульдік заң (Робинсон 1996, Кон 2000 ). Екі қалыпты кіші топ үшін өнім іс жүзінде екеуін қамтитын ең кіші топ болғандықтан, қалыпты топшалар а құрайды модульдік тор.
The Торлы теорема орнатады Галуа байланысы топтың кіші топтарының торы мен оның квотенттері арасындағы.
The Zassenhaus lemma кіші топтардың торындағы квоенттер мен өнімдердің белгілі үйлесімдері арасында изоморфизм береді.
Жалпы алғанда, кез-келген тор қандай да бір топтың ішкі топ торының астарына изоморфты болады деген мағынада топшалардың торына ешқандай шектеу қойылмайды. Сонымен қатар, әрқайсысы ақырлы тор кейбіреулердің топша торының астыңғы қабатына изоморфты ақырғы топ (Шмидт 1994 ж, б. 9)
Сипаттамалық торлар
Белгілі бір қасиеттері бар кіші топтар торлар құрайды, бірақ басқа қасиеттері жоқ.
- Қалыпты топшалар әрқашан модульдік тор құрайды. Шын мәнінде, тордың модульді екендігіне кепілдік беретін маңызды қасиет - бұл топшалардың бір-бірімен жүруі, яғни олардың болуы квазинормальды топшалар.
- Nilpotent қалыпты топшалар тор құрайды, ол (бөлігі) мазмұны болып табылады Фитинг теоремасы.
- Жалпы, кез-келген фитинг сыныбы үшін F, екеуі де субнормальды F- топшалар және қалыпты F-топтар торларды құрайды. Бұл жоғарыда көрсетілгенді қамтиды F нилпотентті топтар класы, сонымен қатар басқа мысалдар F сыныбы шешілетін топтар. Топтар класы, егер ол изоморфизм, субормальды топшалар және субормальды топшалардың өнімдері астында жабық болса, Fitting класы деп аталады.
- Орталық топшалар тор құрайды.
Алайда, ақырғы топшалар да, бұралмалы топтар да тор құрмайды: мысалы тегін өнім екі бұралу элементі арқылы жасалады, бірақ шексіз және құрамында шексіз ретті элементтер бар.
Қалыпты топшалардың модульдік тор құрайтындығы жалпы нәтиженің нақты жағдайы, атап айтқанда кез келген Мальцев әртүрлілігі (олардың қайсысы мысал), сәйкестік торы модульдік (Kearnes & Kiss 2013 ).
Топтарды торшалары бойынша сипаттау
Ішкі топтар туралы тордың теоретикалық ақпаратын кейде бастапқы топ туралы мәлімет беру үшін пайдалануға болады, бұл идея жұмысына оралады. Øистейн кені (1937, 1938 ). Мысалы, руда дәлелдегендей, топ жергілікті циклді егер және оның топшаларының торы болса ғана тарату. Егер тор қосымша өсетін тізбектің шарты, содан кейін топ циклді болады.
Ішкі топтарының торлары а болатын топтар толықтырылған тор деп аталады толықтырылған топтар (Закер 1953 ж ), және топшалары торлары болатын топтар модульдік торлар деп аталады Ивасава топтары немесе модульдік топтар (Ивасава 1941 ж ). Осы типтегі торлы-теоретикалық сипаттамалар үшін де бар шешілетін топтар және тамаша топтар (Suzuki 1951 ).
Әдебиеттер тізімі
- Ашбахер, М. (2000). Соңғы топтық теория. Кембридж университетінің баспасы. б. 6. ISBN 978-0-521-78675-1.CS1 maint: ref = harv (сілтеме)
- Баер, Рейнхольд (1939). «Топтың құрылымы үшін кіші топтар жүйесінің маңызы». Американдық математика журналы. Джонс Хопкинс университетінің баспасы. 61 (1): 1–44. дои:10.2307/2371383. JSTOR 2371383.CS1 maint: ref = harv (сілтеме)
- Кон, Пол Мориц (2000). Классикалық алгебра. Вили. б. 248. ISBN 978-0-471-87731-8.CS1 maint: ref = harv (сілтеме)
- Ивасава, Кенкити (1941), «Über die endlichen Gruppen und die Verbände ihrer Untergruppen», J. Fac. Ғылыми. Имп. Унив. Токио. Секта. I., 4: 171–199, МЫРЗА 0005721CS1 maint: ref = harv (сілтеме)
- Кернс, Кит; Kiss, Emil W. (2013). Конгресстік торлардың пішіні. Американдық математикалық со. б. 3. ISBN 978-0-8218-8323-5.CS1 maint: ref = harv (сілтеме)
- Руда, Øистейн (1937). «Құрылымдар және топтық теория. Мен». Duke Mathematical Journal. 3 (2): 149–174. дои:10.1215 / S0012-7094-37-00311-9. МЫРЗА 1545977.CS1 maint: ref = harv (сілтеме)
- Руда, Øистейн (1938). «Құрылымдар және топтық теория. II». Duke Mathematical Journal. 4 (2): 247–269. дои:10.1215 / S0012-7094-38-00419-3. hdl:10338.dmlcz / 100155. МЫРЗА 1546048.CS1 maint: ref = harv (сілтеме)
- Робинсон, Дерек (1996). Топтар теориясының курсы. Springer Science & Business Media. б. 15. ISBN 978-0-387-94461-6.CS1 maint: ref = harv (сілтеме)
- Роттлендер, Ада (1928). «Nachweis der Existenz nicht-isomorpher Gruppen von gleicher Situation der Untergruppen». Mathematische Zeitschrift. 28 (1): 641–653. дои:10.1007 / BF01181188.CS1 maint: ref = harv (сілтеме)
- Шмидт, Роланд (1994). Топтардың торлары. Математикадан экспозициялар. 14. Вальтер де Грюйтер. ISBN 978-3-11-011213-9.CS1 maint: ref = harv (сілтеме) Шолу Ральф Фриздің Булда жазған. БАЖ 33 (4): 487–492.
- Сузуки, Мичио (1951). «Шекті топтардың топшаларының торында». Американдық математикалық қоғамның операциялары. Американдық математикалық қоғам. 70 (2): 345–371. дои:10.2307/1990375. JSTOR 1990375.CS1 maint: ref = harv (сілтеме)
- Сузуки, Мичио (1956). Топтың құрылымы және оның топшалары торының құрылымы. Берлин: Springer Verlag.
- Яковлев, В. В. (1974). «Топтың топшалары үшін тор изоморфты болатын жағдайлар». Алгебра және логика. 13 (6): 400–412. дои:10.1007 / BF01462952.CS1 maint: ref = harv (сілтеме)
- Закер, Джованни (1953). «Caratterizzazione dei gruppi risolubili d'ordine finito complementati». Rendiconti del Seminario Matematico della Università di Padova. 22: 113–122. ISSN 0041-8994. МЫРЗА 0057878.CS1 maint: ref = harv (сілтеме)


