Ішкі топ - Subgroup
Бұл мақала үшін қосымша дәйексөздер қажет тексеру. (Маусым 2009) (Бұл шаблон хабарламасын қалай және қашан жою керектігін біліп алыңыз) |
| Алгебралық құрылым → Топтық теория Топтық теория |
|---|
 |
|
Негізгі түсініктер |
|
|
|
Модульдік топтар
|
Шексіз өлшемді Өтірік тобы
|
Жылы топтық теория, филиалы математика, берілген топ G астында екілік операция ∗, a ішкі жиын H туралы G а деп аталады кіші топ туралы G егер H сонымен қатар ∗ операциясының шеңберінде топ құрады. Дәлірек айтсақ, H кіші тобы болып табылады G егер шектеу ∗-ден H × H - бұл топтық операция H. Бұл әдетте белгіленеді H ≤ G, «деп оқыңызH кіші тобы болып табылады G".
The тривиалды кіші топ кез-келген топтың кіші тобы {e} тек сәйкестендіру элементінен тұрады.
A тиісті кіші топ топтың G кіші топ болып табылады H бұл а тиісті ішкі жиын туралы G (Бұл, H ≠ G). Әдетте бұл шартты түрде ұсынылады H < G, «деп оқыңызH топшасы болып табылады GКейбір авторлар тривиальды топты дұрыс болудан шығарады (яғни H ≠ {e}).[1][2]
Егер H кіші тобы болып табылады G, содан кейін G деп аталады кейде артық топ туралы H.
Дәл сол анықтамалар көбінесе жалпыға бірдей қолданылады G ерікті болып табылады жартылай топ, бірақ бұл мақалада топтардың топшалары ғана қарастырылады. Топ G кейде тапсырыс берілген жұппен белгіленеді (G, ∗), әдетте операцияны атап көрсету үшін ∗ қашан G бірнеше алгебралық немесе басқа құрылымдарды жүзеге асырады.
Ішкі топтардың негізгі қасиеттері
- Ішкі жиын H топтың G кіші тобы болып табылады G егер ол бос емес болса ғана және жабық өнімдер мен инверсиялар астында. (Жабу шарттары келесі мағынаны білдіреді: әрқашан а және б бар H, содан кейін аб және а−1 сонымен қатар H. Бұл екі шартты бір баламалы шартқа біріктіруге болады: кез келген уақытта а және б бар H, содан кейін аб−1 сонымен қатар H.) Бұл жағдайда H ақырлы, сонда H кіші топ болып табылады егер және егер болса H өнімдердің астында жабық. (Бұл жағдайда әр элемент а туралы H ақырлы циклдік кіші тобын жасайды H, және кері а сол кезде а−1 = аn−1, қайда n реті болып табылады а.)
- Жоғарыда аталған шартты a тұрғысынан айтуға болады гомоморфизм; Бұл, H топтың кіші тобы болып табылады G егер және егер болса H ішкі бөлігі болып табылады G және гомоморфизм бар (яғни, i (а) = а әрқайсысы үшін а) бастап H дейін G.
- The жеке басын куәландыратын кіші топ - бұл топтың идентификациясы: егер G - бұл жеке басы бар топ eG, және H кіші тобы болып табылады G жеке куәлікпен eH, содан кейін eH = eG.
- The кері кіші топтағы элементтің тобы топтағы элементке кері болып табылады: егер H топтың кіші тобы болып табылады G, және а және б элементтері болып табылады H осындай аб = ба = eH, содан кейін аб = ба = eG.
- The қиылысу кіші топтар A және B қайтадан кіші топ болып табылады.[3] The одақ кіші топтар A және B егер ол болса ғана, бұл кіші топ болып табылады A немесе B басқасын қамтиды, өйткені 2 және 3 2Z және 3Z қосылыстарында, бірақ олардың 5 қосындысы жоқ. Тағы бір мысал - жазықтықтағы х осі мен у осінің бірігуі (қосу операциясымен); осы объектілердің әрқайсысы кіші топ болып табылады, бірақ олардың бірігуі жоқ. Бұл сондай-ақ қиылысы дәл сәйкестік болатын екі кіші топтың мысалы ретінде қызмет етеді.
- Егер S ішкі бөлігі болып табылады G, онда құрамында минималды кіші топ бар Sбар барлық кіші топтардың қиылысын алу арқылы табуға болады S; ол ⟨арқылы белгіленедіS⟩ Және деп аталады құрылған кіші топ S. Элементі G ішінде ⟨S⟩ Егер ол тек элементтердің ақырлы туындысы болса ғана S және олардың инверсиялары.
- Әрбір элемент а топтың G циклдық ішкі топты жасайды ⟨а⟩. Егер ⟨а. Болып табылады изоморфты дейін З/nЗ оң сан үшін n, содан кейін n ол үшін ең кіші оң бүтін сан аn = e, және n деп аталады тапсырыс туралы а. Егер ⟨а⟩ Изоморфты З, содан кейін а бар деп айтылады шексіз тәртіп.
- Кез-келген берілген топтың кіші топтары а толық тор қосу деп аталады кіші топтардың торы. (Әзірге шексіз мұнда әдеттегі теориялық қиылысу болып табылады супремум кіші топтардың жиынтығы - бұл кіші топ жасаған жиынтық-теориялық бірлестік емес, кіші топтардың жиынтық-теориялық бірлестігі.) Егер e болып табылады G, содан кейін тривиальды топ {e} болып табылады минимум кіші тобы G, ал максимум топша - топ G өзі.

Козетс және Лагранж теоремасы
Ішкі топ берілген H және кейбір а G-де біз сол косет aH = {ах : сағ жылы H}. Себебі а аударылатын, карта φ: H → aH берілген φ (сағ) = ах Бұл биекция. Сонымен қатар G дәл сол жақ косетода орналасқан H; сол жақ косетиктер - сәйкес келетін эквиваленттік кластар эквиваленттік қатынас а1 ~ а2 егер және егер болса а1−1а2 ішінде H. Сол жақ косетикалардың саны H деп аталады индекс туралы H жылы G және [арқылы белгіленедіG : H].
Лагранж теоремасы шектеулі топ үшін екенін айтады G және кіші топ H,
қайда |G| және |H| белгілеу тапсырыстар туралы G және Hсәйкесінше. Атап айтқанда, кез-келген кіші топтың тәртібі G (және-нің әрбір элементінің реті G) болуы керек бөлгіш |G|.[4][5]
Дұрыс косетиктер ұқсас түрде анықталады: Ха = {ха : сағ жылы H}. Олар сондай-ақ сәйкес эквиваленттік қатынас үшін эквиваленттік кластар болып табылады және олардың саны [G : H].
Егер aH = Ха әрқайсысы үшін а жылы G, содан кейін H деп аталады қалыпты топша. 2 индексінің кез-келген кіші тобы қалыпты: сол жақ косетиктер, сонымен қатар оң косетиктер жай топша және оның толықтырушысы болып табылады. Жалпы, егер б ақырғы топтың ретін бөлетін ең төменгі жай сан G, онда индекстің кез-келген кіші тобы б (егер мұндай болса) қалыпты жағдай.
Мысалы: Z топшалары8
Келіңіздер G болуы циклдік топ З8 оның элементтері
және кімнің топтық операциясы қосу модулі сегіз. Оның Кейли үстелі болып табылады
| + | 0 | 2 | 4 | 6 | 1 | 3 | 5 | 7 |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 2 | 4 | 6 | 1 | 3 | 5 | 7 |
| 2 | 2 | 4 | 6 | 0 | 3 | 5 | 7 | 1 |
| 4 | 4 | 6 | 0 | 2 | 5 | 7 | 1 | 3 |
| 6 | 6 | 0 | 2 | 4 | 7 | 1 | 3 | 5 |
| 1 | 1 | 3 | 5 | 7 | 2 | 4 | 6 | 0 |
| 3 | 3 | 5 | 7 | 1 | 4 | 6 | 0 | 2 |
| 5 | 5 | 7 | 1 | 3 | 6 | 0 | 2 | 4 |
| 7 | 7 | 1 | 3 | 5 | 0 | 2 | 4 | 6 |
Бұл топтың екі бейресми топшасы бар: Дж={0,4} және H={0,2,4,6}, қайда Дж кіші тобы болып табылады H. Cayley кестесі H Cayley кестесінің жоғарғы сол жақ квадранты G. Топ G болып табылады циклдік, және де оның топшалары. Жалпы, циклдік топтардың кіші топтары да циклдік болып келеді.
Мысалы: S топшалары4 ( симметриялық топ 4 элемент бойынша)
Әр топта негізгі диагональ бойынша бейтарап элементтер сияқты шағын топшалар бар:
The тривиальды топ және екі элементті топтар Z2. Бұл кіші топтар келесі тізімде есепке алынбайды.
 The симметриялық топ S4 бәрін көрсету ауыстыру 4 элементтен тұрады |
 Барлық 30 кіші топтар  Жеңілдетілген Диаграммалар туралы кіші топтардың торы С.4 |
12 элемент

8 элемент
 |
 8-ші бұйрық тобы Ішкі топтар: 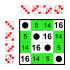  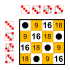 |
 8-ші бұйрық тобы Ішкі топтар: 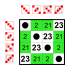  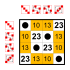 |
6 элемент
 |
 Симметриялық топ S3 Ішкі топ:  |
 Симметриялық топ S3 Ішкі топ:  |
 Симметриялық топ S3 Ішкі топ:  |
4 элемент
 Клейн төрт топтық |
 Клейн төрт топтық |
 Клейн төрт топтық |
 Циклдік топ З4 |
 Циклдық топ Z4 |
 Циклдік топ Z4 |
3 элемент
 Циклдік топ З3 |
 Циклдік топ Z3 |
 Циклдік топ Z3 |
 Циклдік топ Z3 |
Басқа мысалдар
- Жұп сандар - бұл бүтін сандардың аддитивті тобының кіші тобы: екі жұп сандарды қосқанда жұп сан шығады.
- Ан идеалды сақинада қосынды тобының кіші тобы болып табылады .
- A сызықтық ішкі кеңістік а векторлық кеңістік - векторлардың аддитивті тобының кіші тобы.
- Келіңіздер болуы абель тобы; элементтері шектеулі кезең кіші тобын құрайды деп аталады бұралу кіші тобы туралы .
Сондай-ақ қараңыз
Ескертулер
- ^ Хунгерфорд (1974), б. 32
- ^ Артин (2011), б. 43
- ^ Джейкобсон (2009), б. 41
- ^ Қараңыз осы бейнедегі дидактикалық дәлелдеу.
- ^ С., Думмит, Дэвид (2004). Реферат алгебра. Фут, Ричард М., 1950- (3. ред.) Хобокен, НЖ: Вили. б. 90. ISBN 9780471452348. OCLC 248917264.
Әдебиеттер тізімі
- Джейкобсон, Натан (2009), Негізгі алгебра, 1 (2-ші басылым), Довер, ISBN 978-0-486-47189-1.
- Хунгерфорд, Томас (1974), Алгебра (1-ші басылым), Springer-Verlag, ISBN 9780387905181.
- Артин, Майкл (2011), Алгебра (2-ші басылым), Prentice Hall, ISBN 9780132413770.
- С., Думмит, Дэвид (2004). Реферат алгебра. Фут, Ричард М., 1950- (3. ред.) Хобокен, НЖ: Вили. ISBN 9780471452348. OCLC 248917264.



![[G: H] = {| G | аяқталды | H |}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e64b76d0605e6c7891273e65da28b5e431d4ea4)






