Қабаттану - Википедия - Foliation

Бұл мақалада жалпы тізімі бар сілтемелер, бірақ бұл негізінен тексерілмеген болып қалады, өйткені ол сәйкесінше жетіспейді кірістірілген дәйексөздер. Көмектесіңізші жақсарту осы мақала таныстыру дәлірек дәйексөздер. (2014 жылғы қаңтар) (Бұл шаблон хабарламасын қалай және қашан жою керектігін біліп алыңыз)

2 өлшемді бөлімі Риб жапырағы

Риб жапырағының 3 өлшемді моделі

Жылы математика (дифференциалды геометрия ), а жапырақтану болып табылады эквиваленттік қатынас бойынша n-көпқабатты, эквиваленттік сыныптар байланысты, инъекциялық батырылған субманифолдтар, барлығы бірдей өлшем б, үлгісі бойынша ыдырау туралы нақты координаталық кеңістік Rⁿ ішіне ғарыш х + R^б стандартты ендірілген ішкі кеңістік R^б. Эквиваленттік кластар деп аталады жапырақтары жапырақшаның.^[1] Егер коллекторда және / немесе субманифолдтарда а болуы қажет болса кесінді-сызықтық, ажыратылатын (сынып.) C^р), немесе аналитикалық содан кейін құрылым сәйкесінше сызықтық, дифференциалданатын немесе аналитикалық жапырақтарды анықтайды. Сыныптың дифференциалды жапырақтануы ең маңызды жағдайда C^р әдетте мұны түсінеді р ≥ 1 (әйтпесе, C⁰ топологиялық жапырақ).^[2] Нөмір б (жапырақтардың өлшемі) жапырақтың өлшемі деп аталады және q = n − б оның деп аталады кодименция.

Кейбір құжаттарда жалпы салыстырмалылық математикалық физиктер, фолиация термині (немесе кесу) тиісті жағдайды сипаттау үшін қолданылады Лоренц (a (p + 1) -өлшемді ғарыш уақыты ) ыдырады гипер беткейлер өлшем б, нақты бағаланатын деңгей жиынтығы ретінде көрсетілген тегіс функция (скаляр өрісі ) кімнің градиент барлық жерде нөлге тең емес; бұл тегіс функция, әдетте, а деп қабылданады уақыт функциясы, оның градиенті барлық жерде болатындығын білдіреді уақыт тәрізді, сондықтан оның деңгей жиынтығы кеңістікке ұқсас гипер беткейлер болады. Стандартты математикалық терминологияны ескере отырып, бұл гипербетті жиі жапырақ деп атайды (немесе кейде) тілімдер) жапырақтың.^[3] Бұл жағдай стандартты математикалық мағынада кодименция-1 жапырағын құрайтынымен, бұл түрдегі мысалдар іс жүзінде тривиальды екенін ескеріңіз; ал (математикалық) кодименция-1 жапырағының жапырақтары әрқашан жергілікті функциялардың деңгей жиынтықтары, оларды жалпы әлемде осылайша өрнектеу мүмкін емес,^[4][5] өйткені жапырақ локальді-тривиализациялық диаграммадан бірнеше рет өте алады, ал жапырақтың айналасындағы голономия сонымен қатар жапырақтар үшін ғаламдық деңгейге сәйкес анықтайтын функциялардың болуына кедергі келтіруі мүмкін. Мысалы, 3-сферада Риб ашқан әйгілі кодименция-1 жапырағы болса, жабық коллектордың 1 өлшемді фоляциясы тегіс функцияның деңгей жиынтығымен берілмейді, өйткені жабық коллектордағы тегіс функция міндетті түрде максимумдары мен минимумдарында критикалық нүктелері бар.

Қапталған кестелер мен атластар

Қабыршақтарға дәлірек анықтама беру үшін кейбір көмекші элементтерге анықтама беру керек.

3 өлшемді жапырақталған диаграмма n = 3 және q = 1. Бляшкалар 2-өлшемді, ал көлденеңдері 1-өлшемді.

A тікбұрышты Көршілестік жылы Rⁿ болып табылады ашық ішкі жиын форманың B = Дж₁ × ⋅⋅⋅ × Дж_n, қайда Дж_мен ішіндегі салыстырмалы түрде ашық аралық болып табылады (мүмкін шектелмеген) менкоординат осі. Егер Дж₁ формада (а, 0], делінген B бар шекара ^[6]

${ displaystyle жарым-жартылай B = сол жақта {{ сол жақта (0, x ^ {2}, ldots, x ^ {n} right) in B right }.}$

Келесі анықтамада мәні бар координаталық диаграммалар қарастырылады R^б × R^q, шекарасы бар және (дөңес ) бұрыштар.

A жапырақталған диаграмма үстінде n-көпқабатты М кодименция q бұл жұп (U,φ), қайда U ⊆ М ашық және ${ displaystyle varphi: U to B _ { tau} times B _ { pitchfork}}$ Бұл диффеоморфизм, ${ displaystyle B _ { pitchfork}}$ төртбұрышты көршілес болу R^q және ${ displaystyle B _ { tau}}$ ішіндегі тікбұрышты аудан R^б. Жинақ P_ж = φ⁻¹(B_τ × {ж}), қайда ${ displaystyle y in B _ { pitchfork}}$, а деп аталады тақта осы жапырақты кестенің. Әрбір ∈ үшін B_τ, жиынтық S_х = φ⁻¹({х} × ${ displaystyle B _ { pitchfork}}$) а деп аталады көлденең Қабыршылған диаграмма. Жинақ ∂_τU = φ⁻¹(B_τ × (∂${ displaystyle B _ { pitchfork}}$)) деп аталады тангенциалды шекара туралы U және ${ displaystyle kısalt _ { pitchfork} U}$ = φ⁻¹((∂B_τ) × ${ displaystyle B _ { pitchfork}}$) деп аталады көлденең шекара туралы U.^[7]

Қабыршылған диаграмма барлық жапырақтар үшін негізгі модель болып табылады, тақта жапырақтары болып табылады. Белгі B_τ «деп оқыладыB-тангенциалды »және ${ displaystyle B _ { pitchfork}}$ ретінде «Bкөлденең «. Сонымен қатар әр түрлі мүмкіндіктер бар. Егер екеуі де болса ${ displaystyle B _ { pitchfork}}$ және B_τ бос шекарасы бар, кестеленген диаграмма модельдерінің моделі -q жапырақтары n-шексіз көп қатпарлы. Егер бұл төртбұрышты маңайдың екеуінің де шекарасы болмаса, жапырақты диаграмма фольгацияның әртүрлі мүмкіндіктерін модельдейді n-шекпен және бұрышсыз көп қабаттар. Нақтырақ айтқанда, егер ∂${ displaystyle B _ { pitchfork}}$ ≠ ∅ = ∂B_τ, содан кейін .U = ∂_τU тақталардың бірігуі болып табылады және бляшкалардың жапырағы шекараға жанасады. Егер ∂B_τ ≠ ∅ = ∂${ displaystyle B _ { pitchfork}}$, содан кейін .U = ${ displaystyle kısalt _ { pitchfork} U}$ - бұл көлденеңдердің бірігуі және жапырақшасы шекарасына көлденең. Ақырында, егер ∂${ displaystyle B _ { pitchfork}}$ ≠ ∅ ≠ ∂B_τ, бұл тангенциалды шекараны көлденең шекарадан бөлетін бұрышы бар жапырақты коллектордың моделі.^[7]

(а) Шекараға жанама жапырақ ∂${ displaystyle B _ { pitchfork}}$ ≠ ∅ = ∂B_τ; (б) Қабырға шекарасына көлденең ∂B_τ ≠ ∅ = ∂${ displaystyle B _ { pitchfork}}$; (вТангенциалды шекараны көлденең шекарадан бөлетін бұрышпен қабыршақтану ∂${ displaystyle B _ { pitchfork}}$ ≠ ∅ ≠ ∂B_τ.

A жапырақты атлас кодименция q және сынып C^р (0 ≤ р ≤ ∞) n-көпқабатты М Бұл C^р-атлас ${ displaystyle { mathcal {U}} = {(U _ { alpha}, varphi _ { alpha}) mid alpha in A }}$ Кодименцияның жапырақты диаграммаларының q қайсысы жапырақты әрқашан деген мағынада P және Q диаграммаларындағы бляшкалар болып табылады ${ displaystyle { mathcal {U}}}$, содан кейін P ∩ Q ішінде де ашық P және Q.^[8]

Когерентті фолиацияланған диаграмма түсінігін қайта құрудың пайдалы әдісі - жазу w ∈ U_α ∩ U_β ^[9]

${ displaystyle varphi _ { alpha} (w) = left (x _ { alpha} (w), y _ { alpha} (w) right) in B _ { tau} ^ { alpha} рет B _ { pitchfork} ^ { альфа},}$

${ displaystyle varphi _ { beta} (w) = left (x _ { beta} (w), y _ { beta} (w) right) in B _ { tau} ^ { beta} рет B _ { pitchfork} ^ { бета}.}$

Белгі (U_α,φ_α) жиі жазылады (U_α,х_α,ж_α), бірге ^[9]

${ displaystyle x _ { alpha} = left (x _ { alpha} ^ {1}, dots, x _ { alpha} ^ {p} right),}$

${ displaystyle y _ { alpha} = left (y _ { alpha} ^ {1}, dots, y _ { alpha} ^ {q} right).}$

Қосулы φ_β(U_α ∩ U_β) координаттар формуласын келесідей өзгертуге болады ^[9]

${ displaystyle g _ { alpha beta} left (x _ { beta}, y _ { beta} right) = varphi _ { alpha} circ varphi _ { beta} ^ {- 1} солға (х _ { бета}, у _ { бета} оңға) = солға (х _ { альфа} солға (х _ { бета}, у _ { бета} оңға), у _ { альфа} солға (х _ { бета}, у _ { бета} оң) дұрыс).}$

Тақталары U_α әрқайсысының екі тақтасымен кездеседі U_β.

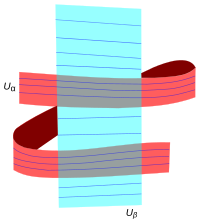
Шарт (U_α,х_α,ж_α) және (U_β,х_β,ж_β) дәйекті түрде жапырақты болу дегеніміз, егер P ⊂ U_α тақтайшасы болып табылады, байланысты компоненттері P ∩ U_β тақталарында (мүмкін болуы мүмкін) U_β. Эквивалентті, өйткені U_α және U_β көлденең координаталардың деңгей жиынтығы ж_α және ж_βсәйкесінше әр пункт з ∈ U_α ∩ U_β формуласы бар көрші бар

${ displaystyle y _ { alpha} = y _ { alpha} (x _ { beta}, y _ { beta}) = y _ { alpha} (y _ { beta})}$

тәуелді емес х_β.^[9]

Қабыршықты атластардың негізгі қолданылуы - олардың жапырақшаларын қалыптастыру үшін олардың қабаттасқан тақталарын байланыстыру. Осы және басқа мақсаттар үшін жоғарыда келтірілген жапырақты атластың жалпы анықтамасы сәл ебедейсіз. Бір мәселе - (U_α,φ_α) (U_β,φ_β). Тіпті бір диаграмма тақтасы басқа диаграмманың көптеген тақтайшаларымен сәйкес келуі мүмкін. Алайда, жағдайды төменде көрсетілгендей әлдеқайда тұрақты деп қабылдауда ешқандай жалпылық жоғалтылмайды.

Қабыршылған екі атлас ${ displaystyle { mathcal {U}}}$ және ${ displaystyle { mathcal {V}}}$ қосулы М бірдей коэффициенттің және тегістік сынып C^р болып табылады келісімді ${ displaystyle left ({ mathcal {U}} thickapprox { mathcal {V}} right)}$ егер ${ displaystyle { mathcal {U}} cup { mathcal {V}}}$ жапырақты C^р-атлас. Қабыршықты атластардың когеренттілігі - эквиваленттік қатынас.^[9]

Дәлел [9]

Рефлексивтілік және симметрия дереу. Дәлелдеу өтімділік рұқсат етіңіз ${ displaystyle { mathcal {U}} thickapprox { mathcal {V}}}$ және ${ displaystyle { mathcal {V}} thickapprox { mathcal {W}}}$. Келіңіздер (Uα,хα,жα) ∈ ${ displaystyle { mathcal {U}}}$ және (Wλ,хλ,жλ) ∈ ${ displaystyle { mathcal {W}}}$ және бір мәселе бар делік w ∈ Uα ∩ Wλ. Таңдау (Vδ,хδ,жδ) ∈ ${ displaystyle { mathcal {V}}}$ осындай w ∈ Vδ. Жоғарыда айтылған ескертулер бойынша, бұл маңда N туралы w жылы Uα ∩ Vδ ∩ Wλ осындай ${ displaystyle y _ { delta} = y _ { delta} (y _ { lambda}) quad { text {on}} quad varphi _ { lambda} (N),}$ ${ displaystyle y _ { alpha} = y _ { alpha} (y _ { delta}) quad { text {on}} quad varphi _ { delta} (N),}$ және демек ${ displaystyle y _ { alpha} = y _ { alpha} left (y _ { delta} (y _ { lambda}) right) quad { text {on}} quad varphi _ { delta} (N).}$ Бастап w ∈ Uα ∩ Wλ ерікті, деген қорытынды жасауға болады жα(хλ,жλ) жергілікті тәуелді емес хλ. Осылайша дәлелденді ${ displaystyle { mathcal {U}} thickapprox { mathcal {W}}}$, демек, келісімділік өтпелі болып табылады.[10]

Кәдімгі жапырақты атласта диаграмма үлгісі.

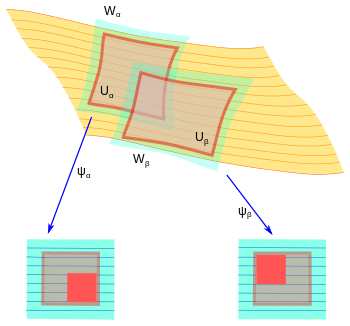
Ашық жиынтықтарда жоғарыда анықталған бляшкалар мен трансверстер де ашық. Сонымен қатар, жабық тақтайшалар мен трансверстальдар туралы айтуға болады. Атап айтқанда, егер (U,φ) және (W,ψ) - бұл бүктелген диаграммалар ${ displaystyle { overline {U}}}$ ( жабу туралы U) ішкі бөлігі болып табылады W және φ = ψ|U содан кейін, егер ${ displaystyle varphi (U) = B _ { tau} times B _ { pitchfork},}$ мұны көруге болады ${ displaystyle psi | { overline {U}}}$, жазылған ${ displaystyle { overline { varphi}}}$, асырады ${ displaystyle { overline {U}}}$ диффеоморфты түрде ${ displaystyle { overline {B}} _ { tau} times { overline {B}} _ { pitchfork}.}$

Қабыршықты атлас дейді тұрақты егер

1. әрбір α ∈ үшін A, ${ displaystyle { overline {U}} _ { alpha}}$ Бұл ықшам жиын жапырақты диаграмманың (W_α,ψ_α) және φ_α = ψ_α|U_α;
2. The қақпақ {U_α | α ∈ A} болып табылады жергілікті шектеулі;
3. егер (U_α,φ_α) және (U_β,φ_β) - бұл жабылған атластың элементтері, содан кейін әр жабық тақтаның ішкі жағы P ⊂ ${ displaystyle { overline {U}} _ { alpha}}$ ең көп дегенде бір тақтада кездеседі ${ displaystyle { overline {U}} _ { beta}.}$ ^[11]

(1) қасиеті бойынша координаттар х_α және ж_α координаталарға дейін кеңейту ${ displaystyle { overline {x}} _ { alpha}}$ және ${ displaystyle { overline {y}} _ { alpha}}$ қосулы ${ displaystyle { overline {U}} _ { alpha}}$ және біреуі жазады ${ displaystyle { overline { varphi}} _ { alpha} = left ({ overline {x}} _ { alpha}, { overline {y}} _ { alpha} right).}$ (3) меншік, егер талап етілсе, балама U_α ∩ U_β ≠ ∅, көлденең координат өзгереді ${ displaystyle { overline {y}} _ { alpha} = { overline {y}} _ { alpha} left ({ overline {x}} _ { beta}, { overline {y}) } _ { бета} дұрыс)}$ тәуелді болмаңыз ${ displaystyle { overline {x}} _ { beta}.}$ Бұл

${ displaystyle { overline {g}} _ { alpha beta} = { overline { varphi}} _ { alpha} circ { overline { varphi}} _ { beta} ^ {- 1 }: { overline { varphi}} _ { beta} left ({ overline {U}} _ { alpha} cap { overline {U}} _ { beta} right) rightarrow { overline { varphi}} _ { alpha} left ({ overline {U}} _ { alpha} cap { overline {U}} _ { beta} right)}$

формуласы бар ^[11]

${ displaystyle { overline {g}} _ { alpha beta} left ({ overline {x}} _ { beta}, { overline {y}} _ { beta} right) = солға ({ сызық {x}} _ { альфа} солға ({ сызықша {x}} _ { бета}, { сызықша {y}} _ { бета} оңға), { сызықша { у}} _ { альфа} сол ({ сызықша {y}} _ { бета} оң) оң).}$

Ұқсас тұжырымдамалар ашық диаграммалар үшін де (сызықтарсыз) қолданылады. Көлденең координаттар картасы ж_α ретінде қарастыруға болады суға бату

${ displaystyle y _ { alpha}: U _ { alpha} rightarrow mathbb {R} ^ {q}}$

және формулалар ж_α = ж_α(ж_β) деп қарауға болады диффеоморфизмдер

${ displaystyle gamma _ { alpha beta}: y _ { beta} left (U _ { alpha} cap U _ { beta} right) rightarrow y _ { alpha} сол жақ (U _ { альфа) } cap U _ { beta} right).}$

Бұлар қанағаттандырады цикл жағдайлары. Яғни ж_δ(U_α ∩ U_β ∩ U_δ),

${ displaystyle гамма _ { альфа дельта} = гамма _ { альфа бета} цир гамма _ { бета дельта}}$

және, атап айтқанда,^[12]

${ displaystyle gamma _ { alpha alpha} equiv y _ { alpha} left (U _ { alpha} right),}$

${ displaystyle гамма _ { альфа бета} = гамма _ { бета альфа} ^ {- 1}.}$

Жоғарыда келтірілген анықтамаларды біртектілік пен жүйелілікке қолдана отырып, кез-келген фолиацияланған атластың когерентті болатындығын дәлелдеуге болады нақтылау бұл тұрақты.^[13]

Дәлел [13]

Көрсеткішті қосыңыз М және жапырақты атлас ${ displaystyle { mathcal {W}}.}$ А өту жасырын, егер қажет болса, мұны болжауға болады ${ displaystyle { mathcal {W}} = left {W_ {j}, psi _ {j} right } _ {j = 1} ^ {l}}$ ақырлы. Ε> 0 а-ға тең болсын Лебег нөмірі үшін ${ displaystyle { mathcal {W}}.}$ Яғни кез-келген ішкі жиын X ⊆ М диаметрі <ε толығымен кейбіреулерінде жатыр Wj. Әрқайсысы үшін х ∈ М, таңдау j осындай х ∈ Wj және жапырақталған диаграмманы таңдаңыз (Uх, φх) солай х ∈ Uх ⊆ ${ displaystyle { overline {U}} _ {x}}$ ⊂ Wj, φх = ψj|Uх, диам (Uх) <ε / 2. Айталық Uх ⊂ Wк, к ≠ j, және жазыңыз ψк = (хк,жк) әдеттегідей, қайда жк : Wк → Rq - көлденең координаттар картасы. Бұл суға бату тақтайшалары бар Wк деңгей жиынтығы ретінде. Осылайша, жк суға батумен шектеледі жк : Uх → Rq. Бұл жергілікті тұрақты хj; сондықтан таңдау Uх кішірек, егер қажет болса, мұны болжауға болады жк|${ displaystyle { overline {U}} _ {x}}$ тақталары бар ${ displaystyle { overline {U}} _ {x}}$ оның деңгейі белгіленеді. Яғни, әрбір тақта Wк ең көп дегенде бір (ықшам) тақтаға сәйкес келеді (демек) ${ displaystyle { overline {U}} _ {x}}$. 1 <бастап к < л <∞, біреуін таңдауға болады Uх сондықтан, қашан болса да Uх ⊂ Wк, анық тақталары ${ displaystyle { overline {U}} _ {x}}$ тақтайшаларында жатыр Wк. Шекті субатласқа өту ${ displaystyle { mathcal {U}} = left {U_ {i}, varphi _ {i} right } _ {i = 1} ^ {N}}$ туралы {(Uх,φх) | х ∈ М}. Егер Uмен ∩ Uj ≠ 0, содан кейін диам (Uмен ∪ Uj) <ε, демек, индекс бар к осындай ${ displaystyle { overline {U}} _ {i} cup { overline {U}} _ {j} subseteq W_ {k}.}$ Арнайы тақтайшалар ${ displaystyle { overline {U}} _ {i}}$ (сәйкесінше, ${ displaystyle { overline {U}} _ {j}}$) тақтайшаларында жатыр Wк. Сондықтан әрбір тақта ${ displaystyle { overline {U}} _ {i}}$ ішкі кеңесінде ең көп дегенде бір тақта бар ${ displaystyle { overline {U}} _ {j}}$ және керісінше. Құрылыс бойынша, ${ displaystyle { mathcal {U}}}$ - бұл келісілген нақтылау ${ displaystyle { mathcal {W}}}$ және әдеттегі жапырақты атлас. Егер М ықшам емес, жергілікті ықшамдылық және екінші есептілік бірізділікті таңдауға мүмкіндік береді ${ displaystyle left {K_ {i} right } _ {i = 0} ^ { infty}}$ ықшам ішкі жиынтығы Қмен ⊂ int Қмен+1 әрқайсысы үшін мен ≥ 0 және ${ displaystyle M = bigcup _ {i = 1} ^ { infty} K_ {i}.}$ Субатласқа өтіп, бұл туралы болжануда ${ displaystyle { mathcal {W}} = left {W_ {j}, psi _ {j} right } _ {j = 0} ^ { infty}}$ есептелетін және қатаң түрде өсетін реттілік болып табылады ${ displaystyle left {n_ {l} right } _ {l = 0} ^ { infty}}$ натурал сандарды осылай табуға болады ${ displaystyle { mathcal {W}} _ {l} = left {W_ {j}, psi _ {j} right } _ {j = 0} ^ {n_ {l}}}$ мұқабалар Қл. Let рұқсат етіңізл арақашықтықты белгілеңіз Қл ∂ дейінҚл+1 және choose таңдаңызл > 0 соншалықты кішкентай, εл <мин {δл/ 2, εл-1} үшін л ≥ 1, ε0 <δ0/ 2, және εл - бұл Лебег нөмірі ${ displaystyle { mathcal {W}} _ {l}}$ (ашық қақпағы ретінде Қл) және үшін ${ displaystyle { mathcal {W}} _ {l + 1}}$ (ашық қақпағы ретінде Қл+1). Дәлірек айтқанда, егер X ⊂ М кездеседі Қл (сәйкесінше, Қл+1) және диам X <εл, содан кейін X кейбір элементтерінде жатыр ${ displaystyle { mathcal {W}} _ {l}}$ (сәйкесінше, ${ displaystyle { mathcal {W}} _ {l + 1}}$). Әрқайсысы үшін х ∈ Қл ${ displaystyle diagdown}$ int Қл-1, салу (Uх,φх) мұны талап ететін ықшам корпусқа қатысты ${ displaystyle { overline {U}} _ {x}}$ ықшам ішкі бөлігі болуы Wj және сол φх = ψj|Uх, кейбір j ≤ nл. Сондай-ақ, сол диамды талап етіңіз${ displaystyle { overline {U}} _ {x}}$ <εл/ 2. Бұрынғыдай, ақырғы ішкі мұқабаға өтіңіз ${ displaystyle left {U_ {i}, varphi _ {i} right } _ {i = n_ {l-1} +1} ^ {n_ {l}}}$ туралы Қл ${ displaystyle diagdown}$ int Қл-1. (Міне, алынды n−1 = 0.) Бұл әдеттегі жапырақты атлас жасайды ${ displaystyle { mathcal {U}} = left {U_ {i}, varphi _ {i} right } _ {i = 1} ^ { infty}}$ бұл нақтылайды ${ displaystyle { mathcal {W}}}$ және сәйкес келеді ${ displaystyle { mathcal {W}}.}$.

Қабыршақтың анықтамалары

Жапырақтанудың бірнеше альтернативті анықтамалары жапырақты алу тәсіліне байланысты болады. Фоляцияға жетудің ең көп тараған тәсілі - бұл ыдырау келесілерге жету

Координаттар функциясы арқылы ыдырау х : U→Rⁿ.

Анықтама. A б-өлшемді, сыныптық C^р ан n-өлшемді коллектор М ыдырауы болып табылады М одағына бөлу қосылған субманифольдтер {L_α}_α∈A, деп аталады жапырақтары жапырақшаның, келесі қасиетімен: Әр нүкте М маңы бар U және жергілікті, сыныптық жүйе C^р координаттар х=(х¹, ⋅⋅⋅, хⁿ) : U→Rⁿ әр жапырақ үшін L_α, компоненттері U ∩ L_α теңдеулермен сипатталады х^б+1= тұрақты, ⋅⋅⋅, хⁿ= тұрақты. Қабыршақты жапырақшамен белгіленеді ${ displaystyle { mathcal {F}}}$={L_α}_α∈A.^[14]

Жапырақ ұғымы фолиация туралы интуитивті ойлауға мүмкіндік береді. Біршама геометриялық анықтама үшін б-өлшемді жапырақтар ${ displaystyle { mathcal {F}}}$ туралы n-көпқабатты М жай коллекция ретінде қарастырылуы мүмкін {М_а} бөлшектелген, біріктірілген, батырылған б-өлшемді субманифолдтар (жапырақ жапырақтары) М, әр нүкте үшін х жылы М, диаграмма бар ${ displaystyle (U, varphi)}$ бірге U гомеоморфты Rⁿ құрамында х әрбір жапырақ, М_а, кездеседі U бос жиында немесе а есептелетін суреттері астындағы ішкі кеңістіктер жиынтығы ${ displaystyle varphi}$ жылы ${ displaystyle varphi (M_ {a} cap U)}$ болып табылады б-өлшемді аффиндік ішкі кеңістіктер кім бірінші n − б координаттары тұрақты.

Жергілікті жерде әрбір жапырақты а суға бату келесілерге мүмкіндік береді

Анықтама. Келіңіздер М және Q өлшемнің көп қырлы болуы n және q≤n сәйкесінше және рұқсат етіңіз f : М→Q су асты болу, яғни функцияның дифференциал дәрежесі ( Якобиан ) болып табылады q. Бұл Жасырын функциялар теоремасы бұл ƒ кодименцияны тудырады -q жапырақ қою М мұнда жапырақтары компоненттері ретінде анықталған f⁻¹(х) үшін х ∈ Q.^[14]

Бұл анықтама a сипаттайды өлшем -б жапырақтану ${ displaystyle { mathcal {F}}}$ туралы n-өлшемді коллектор М бұл жабылған диаграммалар U_мен карталармен бірге

${ displaystyle varphi _ {i}: U_ {i} to mathbb {R} ^ {n}}$

қабаттасқан жұптарға арналған U_мен, U_j The ауысу функциялары φ_иж : Rⁿ → Rⁿ арқылы анықталады

${ displaystyle varphi _ {ij} = varphi _ {j} varphi _ {i} ^ {- 1}}$

нысанды қабылдаңыз

${ displaystyle varphi _ {ij} (x, y) = ( varphi _ {ij} ^ {1} (x), varphi _ {ij} ^ {2} (x, y))}$

қайда х біріншісін білдіреді q = n − б координаттар және ж соңғысын білдіреді б үйлестіреді. Бұл,

${ displaystyle { begin {aligned} varphi _ {ij} ^ {1}: {} & mathbb {R} ^ {q} to mathbb {R} ^ {q} varphi _ {ij } ^ {2}: {} & mathbb {R} ^ {n} to mathbb {R} ^ {p} end {aligned}}}$

Өтпелі функциялардың бөлінуі φ_иж ішіне ${ displaystyle varphi _ {ij} ^ {1} (x)}$ және ${ displaystyle varphi _ {ij} ^ {2} (x, y)}$ бөлігі ретінде су асты толығымен ұқсас болып бөлінуіне ${ displaystyle { overline {g}} _ { alpha beta}}$ ішіне ${ displaystyle { overline {y}} _ { alpha} left ({ overline {y}} _ { beta} right)}$ және ${ displaystyle { overline {x}} _ { alpha} left ({ overline {x}} _ { beta}, { overline {y}} _ { beta} right)}$ тұрақты фолийленген атлас анықтамасының бөлігі ретінде. Бұл әдеттегі жапырақты атластар бойынша жапырақтардың тағы бір анықтамасын жасауға мүмкіндік береді. Осы мақсатта бірінші кезекте кодименцияның кез-келген фолиацияланған атласы болатындығын дәлелдеу керек q бірегей жапырақшамен байланысты ${ displaystyle { mathcal {F}}}$ кодименция q.^[13]

Дәлел [13]

Келіңіздер ${ displaystyle { mathcal {U}} = left {U_ {a}, varphi _ { alpha} right } _ { alpha in A}}$ кодименцияның тұрақты жапырақты атласы болыңыз q. Бойынша эквиваленттік қатынасты анықтаңыз М орнату арқылы х ~ ж егер және бар болса ғана ${ displaystyle { mathcal {U}}}$- тақта P0 осындай х,ж ∈ P0 немесе бірізділік бар L = {P0,P1,⋅⋅⋅,Pб} of ${ displaystyle { mathcal {U}}}$- осындай тақтайшалар х ∈ P0, y ∈ Pб, және Pмен ∩ Pмен-1 ≤ ∅ 1 ∅ мен ≤ б. Кезектілік L а деп аталады ұзындықтағы тақта тізбегі p байланыстырушы х және ж. Бұл жағдайда х,ж ∈ P0, дейді {P0} - ұзындығы 0 қосылатын тақта тізбегі х және ж. ~ Эквиваленттік қатынас екендігі анық. Әрбір эквиваленттілік класы екендігі де түсінікті L тақтайшалар бірлестігі. Бастап ${ displaystyle { mathcal {U}}}$- тақтайшалар бір-бірінің ашық жиынтықтарында ғана қабаттасуы мүмкін, L жергілікті өлшеммен топологиялық батырылған субманифер болып табылады n − q. Бляшкалардың ашық жиынтықтары P ⊂ L жергілікті евклид топологиясының негізін құрайды L өлшем n − q және L осы топологияда нақты байланысты. Мұны тексеру өте маңызды емес L болып табылады Хаусдорф. Мұны көрсету басты мәселе L болып табылады екінші есептелетін. Әр тақта 2-ші есептелетін болғандықтан, дәл солай болады L егер ол көрсетілген болса ${ displaystyle { mathcal {U}}}$-бөлшектер L ең көп дегенде шексіз. Осындай тақтайшаның бірін бекітіңіз P0. Қалыпты, жапырақты атластың анықтамасы бойынша, P0 көптеген басқа тақталармен ғана кездеседі. Бұл тақта тізбектерінің саны өте көп {P0,Pменұзындығы}. Ұзындығы бойынша индукция бойынша б басталатын тақта тізбектерінің P0, ≤ p ұзындықтың тек көп болатындығы дәл осылай дәлелденген. Әрқайсысынан бастап ${ displaystyle { mathcal {U}}}$- тақта L ~ анықтамасына сәйкес, ақырлы тақта тізбегімен басталады P0, бекіту келесідей.

Дәлелдеуде көрсетілгендей, жапырақтың жапырақтары length ұзындықтағы тақта тізбектерінің эквиваленттік кластары болып табылады б олар Хаусдорф топологиялық тұрғыдан батырылған б-өлшемді субманифольдтар. Әрі қарай, жапырақтағы бляшкалардың эквиваленттік қатынасы когерентті фоляцияланған атластардың олардың фоляциямен байланысына қатысты эквиваленттілігінде көрінетіндігі көрсетілген. Нақтырақ айтқанда, егер ${ displaystyle { mathcal {U}}}$ және ${ displaystyle { mathcal {V}}}$ жабылған атластар М және егер ${ displaystyle { mathcal {U}}}$ жапырақшамен байланысты ${ displaystyle { mathcal {F}}}$ содан кейін ${ displaystyle { mathcal {U}}}$ және ${ displaystyle { mathcal {V}}}$ келісілген және егер болса ғана ${ displaystyle { mathcal {V}}}$ сонымен бірге байланысты ${ displaystyle { mathcal {F}}}$.^[10]

Дәлел [10]

Егер ${ displaystyle { mathcal {V}}}$ сонымен бірге байланысты ${ displaystyle { mathcal {F}}}$, әр жапырақ L бірігу болып табылады ${ displaystyle { mathcal {V}}}$- тақтайшалар және ${ displaystyle { mathcal {U}}}$- тақтайшалар. Бұл тақталар топологияның ашық ішкі жиынтығы болып табылады L, демек, бір-бірінің ашық жиынтықтарында қиылысады. Бляшкалар бір-бірімен байланысты болғандықтан, а ${ displaystyle { mathcal {U}}}$- тақта а қиылысу мүмкін емес ${ displaystyle { mathcal {V}}}$-тақ тақта, егер олар жалпы жапырақта жатпаса; сондықтан жапырақты атластар когерентті болады. Керісінше, егер біз мұны білетін болсақ ${ displaystyle { mathcal {U}}}$ байланысты ${ displaystyle { mathcal {F}}}$ және сол ${ displaystyle { mathcal {V}} approx { mathcal {U}}}$, рұқсат етіңіз Q болуы а ${ displaystyle { mathcal {V}}}$- тақта. Егер L жапырағы ${ displaystyle { mathcal {F}}}$ және w ∈ L ∩ Q, рұқсат етіңіз P ∈ L болуы а ${ displaystyle { mathcal {U}}}$- тақта w ∈ P. Содан кейін P ∩ Q болып табылады w жылы Q және P ∩ Q ⊂ L ∩ Q. Бастап w ∈ L ∩ Q ерікті, бұдан шығатыны L ∩ Q ашық Q. Бастап L - бұл ерікті жапырақ, содан шығады Q бөлінетін ашық ішкі жиындарға ыдырайды, олардың әрқайсысының қиылысы Q жапырағымен ${ displaystyle { mathcal {F}}}$. Бастап Q байланысты, L ∩ Q = Q. Соңында, Q ерікті болып табылады ${ displaystyle { mathcal {V}}}$- тақта және т.б. ${ displaystyle { mathcal {V}}}$ байланысты ${ displaystyle { mathcal {F}}}$.

Енді жапырақшалардың арасындағы сәйкестік анық М және олармен байланысты жапырақталған атластар фоляция жиынтығы арасындағы жеке сәйкестікті тудырады М және фолийленген атластардың үйлесімділік кластарының жиынтығы немесе басқаша айтқанда, жапырақтар ${ displaystyle { mathcal {F}}}$ кодименция q және сынып C^р қосулы М кодименцияның фолирленген атластарының когеренттілік класы болып табылады q және сынып C^р қосулы М.^[15] Авторы Зорн леммасы, кез-келген жапырақты атластардың когеренттілік класында ерекше максималды фоляс атласы болатыны анық. Осылайша,

Анықтама. Кодименцияның фоляциясы q және сынып C^р қосулы М максималды жапырақты C^р- код өлшемінің атласы q қосулы М.^[15]

Іс жүзінде, жапырақшаны білдіру үшін салыстырмалы түрде кішкене жапырақталған атлас қолданылады. Әдетте, бұл атлас тұрақты болуы керек.

Диаграммада U_мен, жолақтар х = тұрақты басқа диаграммалардағы жолақтармен сәйкес келеді U_j. Бұл субманифолдтар диаграммадан диаграммаға бірігіп максимум құрайды байланысты инъекциялық батырылған субманифолдтар деп аталады жапырақтары жапырақшаның.

Егер біреу диаграмманы кішірейтсе U_мен оны былай жазуға болады U_ix × U_iy, қайда U_ix ⊂ R^n−б, U_iy ⊂ R^б, U_iyтақтасына гомеоморфты, ал нүктелерінің нүктелері U_ix тақталарды параметрге салыңыз U_мен. Егер біреу таңдайтын болса ж₀ жылы U_iy, содан кейін U_ix × {ж₀} болып табылады U_мен әрбір тақта дәл бір рет қиылысады. Мұны жергілікті деп атайды көлденең бөлім жапырақшаның. Байланысты екенін ескеріңіз монодромия жапырақтың жаһандық көлденең бөлімдері болмауы мүмкін.

Іс р = 0 өте ерекше. Анау C⁰ іс жүзінде пайда болатын жапырақтар әдетте «тегіс жапырақты» болады. Дәлірек айтсақ, олар класқа жатады C^р,0, келесі мағынада.

Анықтама. Қабыршақ ${ displaystyle { mathcal {F}}}$ сыныпқа жатады C^{р, к}, р > к ≥ 0, егер фолийленген атластардың сәйкес когеренттілік класы кәдімгі фолиацияланған атластан тұрса {U_α,х_α,ж_α}_α∈A координата формуласының өзгеруі

${ displaystyle g _ { alpha beta} (x _ { beta}, y _ { beta}) = (x _ { alpha} (x _ { beta}, y _ { beta}), y _ { alpha} ( у _ { бета})).}$

сыныпқа жатады C^к, бірақ х_α сыныпқа жатады C^р координаттарда х_β және оның аралас х_β тапсырыстардың бөлшектері ≤р болып табылады C^к координаттарда (х_β,ж_β).^[16]

Жоғарыда келтірілген анықтама а-ның неғұрлым жалпы тұжырымдамасын ұсынады жапырақталған кеңістік немесе дерексіз ламинация. Біреуі көлденең жолдардың ашық, салыстырмалы түрде ықшам жиынтықтарының жағдайын жеңілдетеді R^q, көлденең координаталарға мүмкіндік беру ж_α олардың құндылықтарын жалпы топологиялық кеңістікте қабылдау З. Бляшкалар әлі де ашық, салыстырмалы түрде ықшам ішкі топшалары R^б, көлденең координат формуласының өзгеруі ж_α(ж_β) үздіксіз және х_α(х_β,ж_β) класс болып табылады C^р координаттарда х_β және оның аралас х_β тапсырыстардың бөлшектері ≤р координаттарында үздіксіз (х_β,ж_β). Әдетте бұл қажет М және З жергілікті ықшам болуға, екінші есептелетін және өлшенетін. Бұл өте жабайы жалпылама болып көрінуі мүмкін, бірақ оның пайдалы болатын мәнмәтіндері бар.^[17]

Холономия

Келіңіздер (М, ${ displaystyle { mathcal {F}}}$) жапырақты көпжақты болуы керек. Егер L жапырағы ${ displaystyle { mathcal {F}}}$ және с бұл жол L, жақын маңдағы жапырақтың жүріс-тұрысы қызықтырады с жылы М. Парақтың тұрғыны интуитивті түрде жолмен жүреді с, барлық жақын жапырақтарды қадағалаңыз. Ол немесе ол (бұдан әрі - деп белгіленеді) с(т)) түсімдер, бұл жапырақтардың кейбіреулері «аршылып», көзге көрінбейтін жерден шығып кетуі мүмкін, қалғандары кенеттен аралыққа түсіп, жақындауы мүмкін L асимптотикалық түрде, басқалары азды-көпті қатар жүруі немесе айналасында жел соғуы мүмкін L жанынан, және т.б.. Егер с цикл болып табылады с(т) бірнеше рет сол нүктеге оралады с(т₀) сияқты т шексіздікке жетеді және әр кезде жапырақтары көрінуге немесе көрінбеуге айналуы мүмкін, және т.б.. Бұл мінез-құлық, тиісті түрде рәсімделген кезде, деп аталады голономия жапырақшаның.

Холономия әр түрлі нақты тәсілдермен жапырақты коллекторларда жүзеге асырылады: жапырақты орамдардың жалпы голономия тобы, жалпы жапырақты коллекторлардың голономия псевдогруппасы, жалпы жапырақты коллекторлардың герминдік голономиясы топоид, жапырақтың герминдік голономия тобы және шексіз голономия тобы. жапырақ.

Қабыршықты байламдар

Холономияның қарапайым жағдайды түсіну жалпы голономия жапырақты орамнан. Бұл а ұғымын жалпылау Пуанкаре картасы.

Қима N және бірінші қайтару картасы f қайда М = S¹ × Д.² және N = Д.².

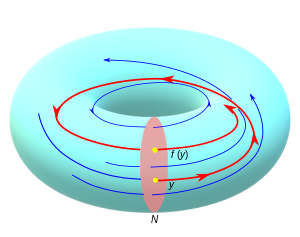
Термин «бірінші қайтару (қайталану) картасы» динамикалық жүйелер теориясынан шығады. Let рұқсат етіңіз_т мағынасыз бол C^р ағын (р ≥ 1) ықшамда n-көпқабатты М. Қолданбаларда мұны елестетуге болады М Бұл циклотрон немесе сұйықтық ағыны бар кейбір тұйық цикл. Егер М шекарасы бар, ағыны шекарасына жанама деп қабылданады. Ағын 1-өлшемді жапырақшаны тудырады ${ displaystyle { mathcal {F}}}$. Егер ағынның оң бағыты есінде болса, бірақ басқаша параметрлеуді ұмытып кетсе (траекторияның пішіні, жылдамдық, және т.б..), негізгі жапырақшалар ${ displaystyle { mathcal {F}}}$ бағдарланған деп айтылады. Ағын ғаламдық көлденең қиманы мойындады делік N. Бұл, N ықшам, дұрыс салынған, C^р субманифолды М өлшем n - 1, жапырақ ${ displaystyle { mathcal {F}}}$ көлденең Nжәне әрбір ағын сызығы сәйкес келеді N. Себебі өлшемдері N жапырақтары бірін-бірі толықтырады, трансверсивтілік шарты сол

${ displaystyle T_ {y} (M) = T_ {y} ({ mathcal {F}}) oplus T_ {y} (N) { text {for each}} y in N}$

Келіңіздер ж ∈ N және қарастыру ω-шектеу орнатылды ω (ж) барлық жинақтау нүктелерінің М барлық тізбектердің ${ displaystyle left { Phi _ {t_ {k}} (y) right } _ {k = 1} ^ { infty}}$, қайда т_к шексіздікке жетеді. Ω (y) ықшам, бос емес және ағын сызықтарының бірігуі екенін көрсетуге болады. Егер ${ displaystyle z = lim _ {k rightarrow infty} Phi _ {t_ {k}} in omega (y),}$ мән бар т* ∈ R осылай Φ_т*(з) ∈ N және осыдан шығады

${ displaystyle lim _ {k to infty} Phi _ {t_ {k} + t ^ { ast}} (y) = Phi _ {t ^ { ast}} (z) in N .}$

Бастап N ықшам және ${ displaystyle { mathcal {F}}}$ көлденең N, {жиынтығы шығадыт > 0 | Φ_т(ж) ∈ N} - бұл монотонды түрде өсетін реттілік ${ displaystyle { tau _ {k} (y) } _ {k = 1} ^ { infty}}$ бұл шексіздікке қарай ауытқиды.

Қалай ж ∈ N өзгереді, рұқсат етіңіз τ(ж) = τ₁(ж), осылайша оң функцияны анықтаймыз τ ∈ C^р(N) (бірінші қайтару уақыты), ерікті түрде ж ∈ N, Φ_т(ж) ∉ N, 0 < т < τ(ж) және Φ_τ(ж)(ж) ∈ N.

Анықтаңыз f : N → N формула бойынша f(ж) = Φ_τ(ж)(ж). Бұл C^р карта. Егер ағын кері болса, дәл сол конструкция кері жағдайды қамтамасыз етеді f⁻¹; сондықтан f Iff Айырмашылық^р(N). Бұл диффеоморфизм бірінші қайтару картасы және τ деп аталады бірінші қайтару уақыты. Бірінші қайтару уақыты ағынның параметрленуіне байланысты болғанымен, бұл айқын болуы керек f тек бағдарланған жапыраққа байланысты ${ displaystyle { mathcal {F}}}$. Ағынды қайта параметрлеуге болады Φ_т, оны классикалық емес C^ржәне оның бағытын өзгертпеу, осылайшаτ ≡ 1.

Ағынның көлденең қимасы бар деген болжам өте шектеулі, сондықтан оны білдіреді М - бұл талшық байламының жалпы кеңістігі S¹. Шынында да R × N, ~ анықтаңыз_f арқылы құрылған эквиваленттік қатынас болу керек

${ displaystyle (t, y) sim _ {f} (t-1, f (y))}$

Эквивалентті түрде, бұл аддитивті топтың әрекеті үшін орбитаның эквиваленттілігі З қосулы R × N арқылы анықталады

${ displaystyle k cdot (t, y) = (t-k, f ^ {k} (y)),}$

әрқайсысы үшін к ∈ З және әрқайсысы үшін (т,ж) ∈ R × N. Картасының цилиндрі f деп анықталды C^р көпжақты

${ displaystyle M_ {f} = ( mathbb {R} times N) / { sim _ {f}}.}$

Бірінші қайтару картасының анықтамасы бойынша f және бірінші қайтару уақыты τ ≡ 1 деп болжанса, карта дереу пайда болады

${ displaystyle Phi: mathbb {R} times N rightarrow M.}$

ағынмен анықталған, канондық индукция жасайды C^р диффеоморфизм

${ displaystyle varphi: M_ {f} rightarrow M.}$

Егер біз сәйкестендіруді жасасақ М_f = М, онда проекциясы R × N үстінде R а тудырады C^р карта

${ displaystyle pi: M rightarrow mathbb {R} / mathbb {Z} = S ^ {1}}$

жасайды М а кеңістігіне талшық байламы шеңбердің үстінен. Бұл жай проекциясы S¹ × Д.² үстінде S¹. Жапырақ ${ displaystyle { mathcal {F}}}$ осы орамның талшықтары мен бума проекциясына көлденең орналасқанπ, әр жапырақпен шектелген L, жабу картасы π : L → S¹. Мұны а деп атайды жапырақталған байлам.

Бастапқы нүкте ретінде алыңыз х₀ ∈ S¹ эквиваленттік класы 0 + З; сондықтан π⁻¹(х₀) бастапқы көлденең қимасы болып табылады N. Әр цикл үшін с қосулы S¹, негізделген х₀, гомотопия класы [с] ∈ π₁(S¹,х₀) градуспен сипатталады с ∈ З. Ілмек с әр ағын сызығындағы жолға көтереді және көтергіш екені түсінікті болуы керек с_ж басталады ж ∈ N аяқталады f^к(ж) ∈ N, қайда к = град с. Диффеоморфизм f^к Iff Айырмашылық^р(N) арқылы да белгіленеді сағ_с және деп аталады жалпы голономия цикл с. Себебі бұл тек [с], бұл гомоморфизмнің анықтамасы

${ displaystyle h: pi _ {1} (S ^ {1}, x_ {0}) rightarrow operatorname {Diff} ^ {, r} (N),}$

деп аталады жалпы голономиялық гомоморфизм жапырақталған байлам үшін.

Талшықты байламдарды тікелей қолдану арқылы,М,${ displaystyle { mathcal {F}}}$) жапырақты болу n-кодименциялардың көп қабаты q. Келіңіздер π : М → B талшықты байлам болыңыз q-өлшемді талшық F және қосылған кеңістік B. Осы құрылымдардың барлығы кластық деп есептейік C^р, 0 ≤ р If ∞, егер болса р = 0, B қолдайды C¹ құрылым. Әрбір максималды болғандықтан C¹ атлас қосулы B құрамында а C^∞ субатлас, бұл туралы ешқандай жалпылық жоғалып кетпейді B қалағандай тегіс. Соңында, әрқайсысы үшін х ∈ B, байланысты, ашық көршілік бар деп есептеңіз U ⊆ B туралы х және жергілікті тривиализация

${ displaystyle { begin {matrix} pi ^ {- 1} (U) & { xrightarrow { varphi}} & U times {F} scriptstyle { pi} { Bigg downarrow} & { qquad} & { Bigg downarrow} { scriptstyle {p}} U & { xrightarrow { text {id}}} & U end {matrix}}}$

қайда φ Бұл C^р диффеоморфизм (гомеоморфизм, егер болса) р = 0) тасымалдайды ${ textstyle { mathcal {F}} mid pi ^ {- 1} (U)}$ өнімнің жапырағына {U × {ж}}_ж ∈ F. Мұнда, ${ textstyle { mathcal {F}} mid pi ^ {- 1} (U)}$ жалғанған компоненттердің жапырақтары арқылы жапырақтануы L ∩ π⁻¹(U), қайда L жапырақтары үстінде орналасқан ${ displaystyle { mathcal {F}}}$. Бұл «жапырақталған шоқ» терминінің жалпы анықтамасы (М,${ displaystyle { mathcal {F}}}$, π) сынып C^р.

${ displaystyle { mathcal {F}}}$ π талшықтарына көлденең орналасқан (осылай дейді) ${ displaystyle { mathcal {F}}}$ фибрацияға көлденең) және әрбір жапыраққа π шектелуі L туралы ${ displaystyle { mathcal {F}}}$ жабу картасы π: L → B. Атап айтқанда, әр талшық F_х = π⁻¹(х) әр жапырағымен кездеседі ${ displaystyle { mathcal {F}}}$. Талшық - көлденең қимасы ${ displaystyle { mathcal {F}}}$ ағынның көлденең қимасы ұғымымен толық ұқсастықта.

Жапырақ ${ displaystyle { mathcal {F}}}$ талшықтарға көлденең болу өздігінен жапырақтың кеңістікті жауып тұрғанына кепілдік бермейді B. Мәселенің қарапайым нұсқасы - бұл фолиация R², фибрацияға көлденең

${ displaystyle pi: mathbb {R} ^ {2} rightarrow mathbb {R},}$

${ displaystyle pi (x, y) = x,}$

бірақ көптеген жапырақтары жоқ ж-аксис. Тиісті суретте «жебе» жапырақтары және олардың үстінде оське асимптотикалық болу көзделген х = 0. Мұндай жапырақты фибрацияға қатысты толық емес деп атайды, яғни кейбір жапырақтар параметр ретінде «шексіздікке қарай ағып кетеді». х ∈ B кейбіріне жақындайды х₀ ∈ B. Дәлірек айтқанда, жапырақ болуы мүмкін L және үздіксіз жол с : [0,а) → L осындай лим_т→а−π (с(т)) = х₀ ∈ B, бірақ лим_т→а−с(т) көптеген топологиясында жоқ L. Бұл кейбір ағын сызықтары ақырғы уақытта «шексіздікке жететін» толық емес ағындардың жағдайына ұқсас. Мұндай жапырақ болса да L басқа жерде кездесуі мүмкін π⁻¹(х₀), оның маңын біркелкі қамтуы мүмкін емес х₀, демек, жабық кеңістік бола алмайды B астында π. Қашан F ықшам, дегенмен, көлденеңдігі ${ displaystyle { mathcal {F}}}$ фибрацияға толықтығы кепілдік береді, демек ${ textstyle (M, { mathcal {F}}, pi)}$ жапырақталған байлам.

Атлас бар ${ displaystyle { mathcal {U}}}$ = {U_α,х_α}_α∈A қосулы B, тривиализациялармен бірге ашық, байланысты координаттар диаграммаларынан тұрады φ_α : π⁻¹(U_α) → U_α × F тасымалдау ${ displaystyle { mathcal {F}}}$| π⁻¹(U_α) өнімнің жапырағына. Орнатыңыз W_α = π⁻¹(U_α) және жазыңыз φ_α = (х_α,ж_α) қайда (белгілерді теріс пайдалану арқылы) х_α ұсынады х_α ∘ π және ж_α : π⁻¹(U_α) → F - композиторлық жолмен алынған суасты φ_α канондық проекциямен U_α × F → F.

Атлас ${ displaystyle { mathcal {W}}}$ = {W_α,х_α,ж_α}_α∈A фольга тәрізді атлас сияқты рөл атқарады. Тақталары W_α деңгейлер жиынтығы болып табылады ж_α және бұл тақта тақтасына ұқсас F арқылы ж_α. Бастап B қолдайды деп болжанған C^∞ сәйкес құрылымы Уайтхед теоремасы Риман метрасын түзетуге болады B және атласты таңдаңыз ${ displaystyle { mathcal {U}}}$ геодезиялық дөңес болуы керек. Осылайша, U_α ∩ U_β әрқашан байланысты. Егер бұл қиылысу бос болмаса, онда әр тақта W_α дәл бір тақтаға сәйкес келеді W_β. Содан кейін a анықтаңыз холономия коксілі ${ displaystyle gamma = left { gamma _ { alpha beta} right } _ { alpha, beta in A}}$ орнату арқылы

${ displaystyle gamma _ { alpha beta} = y _ { alpha} circ y _ { beta} ^ {- 1}: F rightarrow F.}$

Мысалдар

Тегіс кеңістік

Қарастырайық n-өлшемді кеңістік, бірінші болып саналатын нүктелерден тұратын ішкі кеңістіктер көбейтіндісі ретінде көбейтіледі n − б координаттары тұрақты. Мұны жалғыз диаграммамен жабуға болады. Мәлімдеме мәні бойынша Rⁿ = R^n−б × R^б жапырақтармен немесе бляшкалармен R^б санамаланған R^n−б. Ұқсастық қабылдау арқылы үш өлшемде тікелей көрінеді n = 3 және б = 2: кітаптың 2 өлшемді парақтары (1 өлшемді) бет нөмірімен есептеледі.

Бумалар

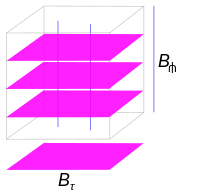
Қабыршақтардың болмашы мысалы - өнім М = B × F, жапырақтары арқылы жапырақты F_б = {б} × F, б ∈ B. (Тағы бір жапырақ М арқылы беріледі B_f = B × { F } ,  F  ∈ F.)

Жалпы сынып тегіс G-бумалар G = Гомео (F) коллектор үшін F. Берілген өкілдік ρ : π₁(B) → Гомео (F), пәтер Гомео (F)-монодромиямен байланыстыру ρ арқылы беріледі ${ displaystyle M = left ({ widetilde {B}} times F right) / pi _ {1} B}$, қайда π₁(B) бойынша әрекет етеді әмбебап қақпақ ${ displaystyle { widetilde {B}}}$ арқылы палубалық түрлендірулер және т.б. F ұсыну арқылы ρ.

Жалпақ байламдар шеңберіне сәйкес келеді талшық байламдары. Карта π : М → B коллекторлар арасында талшықты байлам болып табылады, егер F әр түрлі коллекторы болса б ∈ B ашық маңы бар U гомеоморфизм болатын сияқты ${ displaystyle varphi: pi ^ {- 1} (U) - U есе F}$ бірге ${ displaystyle pi = p_ {1} varphi}$, бірге б₁ : U × F → U проекциясы бірінші факторға дейін. The fiber bundle yields a foliation by fibers ${displaystyle F_{b}:=pi ^{-1}({b}),bin B}$. Its space of leaves L is homeomorphic to B, in particular L is a Hausdorff manifold.

Coverings

Егер М → N Бұл жабу картасы between manifolds, and F is a foliation on N, then it pulls back to a foliation on М. More generally, if the map is merely a branched covering, where the branch локус is transverse to the foliation, then the foliation can be pulled back.

Submersions

Егер Мⁿ → N^q, (q ≤ n) Бұл суға бату of manifolds, it follows from the кері функция теоремасы that the connected components of the fibers of the submersion define a codimension q foliation of М. Талшық байламдары are an example of this type.

An example of a submersion, which is not a fiber bundle, is given by

${displaystyle {egin{cases}f:[-1,1] imes mathbb {R} o mathbb {R} f(x,y)=(x^{2}-1)e^{y}end{cases}}}$

This submersion yields a foliation of [−1, 1] × R which is invariant under the З-actions given by

${displaystyle z(x,y)=(x,y+n),quad { ext{or}}quad z(x,y)=left((-1)^{n}x,y ight)}$

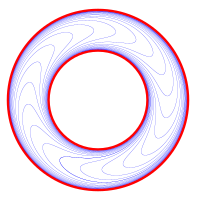
үшін (х, ж) ∈ [−1, 1] × R және n ∈ З. The induced foliations of З \ ([−1, 1] × R) are called the 2-dimensional Reeb foliation (of the annulus) resp. the 2-dimensional nonorientable Reeb foliation (of the Möbius band). Their leaf spaces are not Hausdorff.

Reeb foliations

Define a submersion

${displaystyle {egin{cases}f:D^{n} imes mathbb {R} o mathbb {R} f(r, heta ,t):=(r^{2}-1)e^{t}end{cases}}}$

қайда (р, θ) ∈ [0, 1] × Sⁿ⁻¹ are cylindrical coordinates on the n-dimensional disk Д.ⁿ. This submersion yields a foliation of Д.ⁿ × R which is invariant under the З-actions given by

${displaystyle z(x,y)=(x,y+z)}$

үшін (х, ж) ∈ Д.ⁿ × R, з ∈ З. The induced foliation of З \ (Д.ⁿ × R) деп аталады n-өлшемді Reeb foliation. Its leaf space is not Hausdorff.

Үшін n = 2, this gives a foliation of the solid torus which can be used to define the Reeb foliation of the 3-sphere by gluing two solid tori along their boundary. Foliations of odd-dimensional spheres S²ⁿ⁺¹ are also explicitly known.^[18]

Өтірік топтар

Егер G Бұл Өтірік тобы, және H Бұл Lie кіші тобы, содан кейін G is foliated by ғарыш туралы H. Қашан H болып табылады жабық жылы G, кеңістік G/H is a smooth (Хаусдорф ) manifold turning G into a fiber bundle with fiber H және негіз G/H. This fiber bundle is actually негізгі, with structure group H.

Lie group actions

Келіңіздер G be a Lie group acting smoothly on a manifold М. If the action is a locally free action немесе free action, then the orbits of G define a foliation of М.

Linear and Kronecker foliations

Егер ${displaystyle { ilde {X}}}$ is a nonsingular (яғни, nowhere zero) vector field, then the local flow defined by ${displaystyle { ilde {X}}}$ patches together to define a foliation of dimension 1. Indeed, given an arbitrary point х ∈ М, the fact that ${displaystyle { ilde {X}}}$ is nonsingular allows one to find a coordinate neighborhood (U,х¹,...,хⁿ) туралы х осындай

${displaystyle -varepsilon$

және

${displaystyle {frac {partial }{partial x^{1}}}={ ilde {X}}mid U.}$

Geometrically, the flow lines of ${displaystyle { ilde {X}}mid U}$ are just the level sets

${displaystyle x^{i}=c^{i},quad 2leq ileq n,}$

where all ${displaystyle |c^{i}|$ Since by convention manifolds are second countable, leaf anomalies like the "long line" are precluded by the second countability of М өзі. The difficulty can be sidestepped by requiring that ${displaystyle { ilde {X}}}$ be a complete field (мысалы, сол М be compact), hence that each leaf be a flow line.

The linear foliation ${displaystyle {mathcal { ilde {F}}}}$ қосулы R² passes to the foliation ${ displaystyle { mathcal {F}}}$ қосулы Т². a) the slope is rational (linear foliation); b) the slope is irrational (Kronecker foliation).

Irrational rotation on a 2-torus.

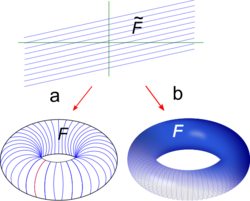
An important class of 1-dimensional foliations on the torus Т² are derived from projecting constant vector fields on Т². A constant vector field

${displaystyle { ilde {X}}equiv {egin{bmatrix}aend{bmatrix}}}$

қосулы R² is invariant by all translations in R², hence passes to a well-defined vector field X when projected on the torus Т²= R²/З². Болжам бойынша а ≠ 0. The foliation ${displaystyle {mathcal { ilde {F}}}}$ қосулы R² өндірілген ${displaystyle { ilde {X}}}$ has as leaves the parallel straight lines of slope θ = б/а. This foliation is also invariant under translations and passes to the foliation ${ displaystyle { mathcal {F}}}$ қосулы Т² өндірілген X.

Each leaf of ${displaystyle {mathcal { ilde {F}}}}$ формада болады

${displaystyle { ilde {L}}={(x_{0}+ta,y_{0}+tb}_{tin mathbb {R} }.}$

If the slope is рационалды then all leaves are closed curves гомеоморфты дейін шеңбер. In this case, one can take а,б ∈ З. Бекітілген үшін т ∈ R, тармақтары ${displaystyle { ilde {L}}}$ corresponding to values of т ∈ т₀ + З all project to the same point of Т²; so the corresponding leaf L туралы ${ displaystyle { mathcal {F}}}$ is an embedded circle in Т². Бастап L is arbitrary, ${ displaystyle { mathcal {F}}}$ is a foliation of Т² by circles. It follows rather easily that this foliation is actually a fiber bundle π : Т² → S¹. Бұл а ретінде белгілі linear foliation.

When the slope θ = б/а болып табылады қисынсыз, the leaves are noncompact, homeomorphic to the non-compactified нақты сызық, және тығыз in the torus (cf Иррационалды айналу ). The trajectory of each point (х₀,ж₀) never returns to the same point, but generates an "everywhere dense" winding about the torus, i.e. approaches arbitrarily close to any given point. Thus the closure to the trajectory is the entire two-dimensional torus. This case is named Kronecker foliation, кейін Леопольд Кронеккер және оның

Kronecker's Density Theorem. If the real number θ is distinct from each rational multiple of π, then the set {e^inθ | n ∈ З} is dense in the unit circle.

Дәлел

To see this, note first that, if a leaf ${displaystyle { ilde {L}}}$ туралы ${displaystyle {mathcal { ilde {F}}}}$ does not project one-to-one into Т2, there must be a real number т ≠ 0 such that та және тб are both integers. But this would imply that б/а ∈ Q. In order to show that each leaf L туралы ${ displaystyle { mathcal {F}}}$ тығыз Т2, it is enough to show that, for every v ∈ R2, each leaf ${displaystyle { ilde {L}}}$ туралы ${displaystyle {mathcal { ilde {F}}}}$ achieves arbitrarily small positive distances from suitable points of the coset v + З2. A suitable translation in R2 allows one to assume that v = 0; so the task is reduced to showing that ${displaystyle { ilde {L}}}$ passes arbitrarily close to suitable points (n,м) ∈ З2. Сызық ${displaystyle { ilde {L}}}$ has slope-intercept equation ${displaystyle y= heta x+c.}$ So it will suffice to find, for arbitrary η > 0, integers n және м осындай ${displaystyle | heta n+c-m|$ Эквивалентті, в ∈ R being arbitrary, one is reduced to showing that the set {θn − м}м,n∈З тығыз R. This is essentially the criterion of Евдокс that θ and 1 be incommensurable (яғни, that θ be irrational).

A similar construction using a foliation of Rⁿ by parallel lines yields a 1-dimensional foliation of the n-торус Rⁿ/Зⁿ байланысты linear flow on the torus.

Suspension foliations

A flat bundle has not only its foliation by fibres but also a foliation transverse to the fibers, whose leaves are

${displaystyle L_{f}:=left{pleft({ ilde {b}},f ight):{ ilde {b}}in {widetilde {B}} ight},quad {mbox{ for }}fin F,}$

қайда ${displaystyle p:{widetilde {B}} imes F o M}$ канондық проекция болып табылады. This foliation is called the suspension of the representation ρ : π₁(B) → Homeo(F).

Атап айтқанда, егер B = S¹ және ${displaystyle varphi :F o F}$ is a homeomorphism of F, then the suspension foliation of ${ displaystyle varphi}$ is defined to be the suspension foliation of the representation ρ : З → Homeo(F) берілген ρ(з) = Φ^з. Its space of leaves is L = ${ displaystyle { mathcal {F}}}$/~, қайда х ~ ж қашан болса да ж = Φⁿ(х) кейбіреулер үшін n ∈ З.

The simplest example of foliation by suspension is a manifold X өлшем q. Келіңіздер f : X → X be a bijection. One defines the suspension М = S¹ ×_f X as the quotient of [0,1] × X by the equivalence relation (1,х) ~ (0,f(х)).

М = S¹ ×_f X = [0,1] × X

Then automatically М carries two foliations: ${ displaystyle { mathcal {F}}}$₂ consisting of sets of the form F_2,т = {(т,х)_~ : х ∈ X} және ${ displaystyle { mathcal {F}}}$₁ consisting of sets of the form F_2,х0 = {(т,х) : т ∈ [0,1] ,х ∈ O_х0}, where the orbit O_х0 ретінде анықталады

O_х0 = {..., f⁻²(х₀), f⁻¹(х₀), х₀, f(х₀), f²(х₀), ...},

where the exponent refers to the number of times the function f is composed with itself. Note that O_х0 = O_f(х0) = O_f⁻²(х0), etc., so the same is true for F_1,х0. Understanding the foliation ${ displaystyle { mathcal {F}}}$₁ is equivalent to understanding the dynamics of the map f. If the manifold X is already foliated, one can use the construction to increase the codimension of the foliation, as long as f maps leaves to leaves.

The Kronecker foliations of the 2-torus are the suspension foliations of the rotations R_α : S¹ → S¹ by angle α ∈ [0, 2π).

Suspension of 2-holed torus after cutting and re-gluing. a) Two-holed torus with the sections to be cut; b) the geometric figure after cutting with the four faces.

More specifically, if Σ = Σ₂ is the two-holed torus with C¹,C² ∈ Σ the two embedded circles let ${ displaystyle { mathcal {F}}}$ be the product foliation of the 3-manifold М = Σ × S¹ with leaves Σ × {ж}, ж ∈ S¹. Ескертіп қой N_мен = C_мен × S¹ is an embedded torus and that ${ displaystyle { mathcal {F}}}$ is transverse to N_мен, мен = 1,2. Let Diff₊(S¹) denote the group of orientation-preserving diffeomorphisms of S¹ and choose f₁,f₂ ∈ Diff₊(S¹). Кесу М apart along N₁ және N₂, letting ${displaystyle N_{i}^{+}}$ және ${displaystyle N_{i}^{-}}$ denote the resulting copies of N_мен, мен = 1,2. At this point one has a manifold M ' = Σ' × S₁ with four boundary components ${displaystyle left{N_{i}^{pm } ight}_{i=1,2}.}$ The foliation ${ displaystyle { mathcal {F}}}$ has passed to a foliation ${displaystyle {mathcal {F^{prime }}}}$ transverse to the boundary ∂M ' , each leaf of which is of the form Σ' × {ж}, ж ∈ S¹.

This leaf meets ∂M ' in four circles ${displaystyle C_{i}^{pm } imes {y}subset N_{i}^{pm }.}$ Егер з ∈ C_мен, the corresponding points in ${displaystyle C_{i}^{pm }}$ деп белгіленеді з^± және ${displaystyle N_{i}^{-}}$ is "reglued" to ${displaystyle N_{i}^{+}}$ by the identification

${displaystyle (z^{-},y)equiv (z^{+},f_{i}(y)),quad i=1,2.}$

Бастап f₁ және f₂ are orientation-preserving diffeomorphisms of S¹, олар сәйкестілікке изотопты болып табылады және осы регулирлеу операциясының нәтижесінде алынған коллектор гомеоморфты болып табылады М. Жапырақтары ${ displaystyle { mathcal {F ^ { prime}}}}$дегенмен, жаңа жапырақты шығару үшін жинаңыз ${ displaystyle { mathcal {F}}}$(f₁,f₂) of М. Егер жапырақ болса L туралы ${ displaystyle { mathcal {F}}}$(f₁,f₂) contains '× {бөлігі барж₀}, содан кейін

${ displaystyle L = bigcup _ {g in G} Sigma ^ { prime} times {g (y_ {0}) },}$

қайда G Iff Айырмашылық₊(S¹) - бұл {f₁,f₂}. Бұл copies 'көшірмелері сәйкестендіру арқылы бір-біріне бекітіледі

(з⁻,ж(ж₀)) ≡ (з⁺,f₁(ж(ж₀))) әрқайсысы үшін з ∈ C₁,

(з⁻,ж(ж₀)) ≡ (з⁺,f₂(ж(ж₀))) әрқайсысы үшін з ∈ C₂,

қайда ж аралықтары аяқталды G. Жапырақ толығымен анықталады G-орбиттің ж₀ ∈ S¹ және ол қарапайым немесе өте күрделі болуы мүмкін. Мысалы, жапырақ дәл сәйкес келсе, ықшам болады G-орбит ақырлы. Шектен тыс мысал ретінде, егер G маңызды емес (f₁ = f₂ = идентификатор_S¹), содан кейін ${ displaystyle { mathcal {F}}}$(f₁,f₂) = ${ displaystyle { mathcal {F}}}$. Егер орбита тығыз болса S¹, сәйкес жапырақ тығыз М. Мысал ретінде, егер f₁ және f₂ бұл 2π-ге тең рационалды тәуелсіз еселіктер арқылы айналу, әр жапырақ тығыз болады. Басқа мысалдарда, кейбір парақтар L жабылуы бар ${ displaystyle { bar {L}}}$ әрбір факторға сәйкес келетін {w} × S¹ ішінде Кантор орнатылды. Ұқсас конструкцияларды Σ × өлшемінде жасауға болады Мен, қайда Мен ықшам, анық емес интервал. Мұнда біреу керек f₁,f₂ Iff Айырмашылық₊(Мен) және, өйткені ∂Мен барлық бағытты сақтайтын дифеоморфизмдермен нүктелік бағытта бекітілген, one екі компоненті бар жапырақты алады.М жапырақ сияқты. Біреуі пайда болған кезде M ' бұл жағдайда бұрыштары бар жапырақты коллектор пайда болады. Екі жағдайда да бұл құрылыс деп аталады тоқтата тұру диффеоморфизмдер жұбы және кодименция-бір жапырақтардың қызықты мысалдарының құнарлы көзі болып табылады.

Қабыршақтар және интегралдылық

Барлығын қабылдаған кезде тығыз қарым-қатынас бар тегіс, бірге векторлық өрістер: векторлық өріс берілген X қосулы М бұл ешқашан нөлге тең емес, оның интегралды қисықтар 1-өлшемді жапырақ береді. (яғни кодименция n − 1 жапырақ).

Бұл байқау жалпыланған Фробениус теоремасы деп, қажетті және жеткілікті шарттар үлестіру үшін (яғни n − б өлшемді қосалқы жинақ туралы тангенс байламы жапырақтың жапырақтарына жанама болу үшін, үлестірімге жанасатын векторлық өрістер жиыны астында жабылады Жалған жақша. Сұрақ ретінде мұны басқаша айтуға болады құрылым тобының қысқаруы туралы тангенс байламы бастап GL (n) төмендетілетін кіші топқа.

Фробениус теоремасындағы жағдайлар келесідей көрінеді интеграциялану шарттары; және егер бұл орындалса, қысқарту қажет блок құрылымымен жергілікті ауысу функциялары болғандықтан орын алуы мүмкін. Мысалы, 1 өлшемді жағдайда, біз жапырақтың жанама шоғырын келесідей анықтай аламыз кер (α), кейбіреулер үшін (канондық емес) α ∈ Ω¹ (яғни нөлдік емес ко-векторлық өріс). Берілген α iff интегралды α ∧ dα = 0 барлық жерде.

Топологиялық шектеулер бар болғандықтан жаһандық жапырақтану теориясы бар. Мысалы, беті жағдайда, барлық жерде нөлдік емес векторлық өріс болады бағдарлы ықшам беті тек торус. Бұл салдар Пуанкаре - Хопф индексі теоремасы көрсетеді, бұл Эйлерге тән болуы керек. көптеген терең байланыстар бар байланыс топологиясы, бұл «қарама-қарсы» ұғым.

Қабыршақтардың болуы

Хафлигер (1970) жалғанған жинақы емес коллектордағы үлестірудің интегралданатын үлестіруге гомотопты болуы үшін қажетті және жеткілікті шарт берді. Терстон (1974, 1976 ) үлестірілімімен кез-келген ықшам коллектордың бірдей өлшемді фоляциясы болатындығын көрсетті.

Сондай-ақ қараңыз

• G құрылымы
• Гельбригер құрылымы, кері қайтарып алу кезінде жабылған жапырақтарды жалпылау.
• Ламинация
• Риб жапырағы 3-сфераның
• Жапырақты жабыңыз

Ескертулер

Әдебиеттер тізімі

• Аносов, Д.В. (2001) [1994], «Қабыршақтану», Математика энциклопедиясы, EMS Press
• Кандел, Альберто; Конлон, Лоуренс (2000). Қабыршақтар I. Математика бойынша магистратура. 23. Провиденс, Род-Айленд: Американдық математикалық қоғам. ISBN  0-8218-0809-5.
• Кандел, Альберто; Конлон, Лоуренс (2003). Қабыршақтар II. Математика бойынша магистратура. 60. Провиденс, Род-Айленд: Американдық математикалық қоғам. ISBN  0-8218-0809-5.
• Гургульхон, Эрик (2012). Жалпы салыстырмалылықтағы 3 + 1 формализм. Физикадан дәрістер. 846. Гейдельберг, Нью-Йорк, Дордрехт, Лондон: Спрингер. дои:10.1007/978-3-642-24525-1. ISBN  978-3-642-24524-4.
• Haefliger, André (1970), «Feuilletages sur les variétés ouvertes», Топология, 9 (2): 183–194, дои:10.1016/0040-9383(70)90040-6, ISSN  0040-9383, МЫРЗА  0263104
• Лоусон, Х.Блейн (1974), «Қабыршақтар», Американдық математикалық қоғамның хабаршысы, 80 (3): 369–418, дои:10.1090 / S0002-9904-1974-13432-4, ISSN  0002-9904, МЫРЗА  0343289
• Moerdijk, Иеке; Mrčun, J. (2003), Фолиация және өтірік топоидтармен таныстыру, Тереңдетілген математика бойынша Кембридж оқулары, 91, Кембридж университетінің баспасы, ISBN  978-0-521-83197-0, МЫРЗА  2012261
• Риб, Джордж (1952), Sur certaines propriétés topologiques des variétés feuilletées, Ғылыми зерттеулер. Инд., Жоқ. 1183, Герман және Ци., Париж, МЫРЗА  0055692
• Терстон, Уильям (1974), «Кодименцияның фоляция теориясы бірден үлкен», Mathematici Helvetici түсініктемелері, 49: 214–231, дои:10.1007 / BF02566730, ISSN  0010-2571, МЫРЗА  0370619
• Терстон, Уильям П. (1976), «Кодименция-бір жапырақтардың болуы», Математика жылнамалары, Екінші серия, жылнамалар, 104 (2): 249–268, дои:10.2307/1971047, ISSN  0003-486X, JSTOR  1971047, МЫРЗА  0425985

Сыртқы сілтемелер

• Қабыршақтар Манифольд Атласында