Бұрыш - Angle

Жылы Евклидтік геометрия, an бұрыш - бұл екеуі құрған фигура сәулелер, деп аталады жақтары деп аталатын жалпы соңғы нүктемен бөлісетін бұрыштың шың бұрыштың.[1]Екі сәуледен пайда болған бұрыштар ұшақ құрамында сәулелер бар. Бұрыштар екі жазықтықтың қиылысуынан да пайда болады. Бұлар аталады екі жақты бұрыштар. Екі қиылысқан қисықтар бұрышы болатын бұрышты анықтаңыз тангенстер қиылысу нүктесінде. Мысалы, сфералық бұрыш екеуі құрған үлкен үйірмелер үстінде сфера үлкен дөңгелектері бар жазықтықтар арасындағы диедралды бұрышқа тең.
Бұрыш белгілеу үшін де қолданылады өлшеу бұрышының немесе а айналу. Бұл өлшем - а ұзындығының қатынасы дөңгелек доға оған радиусы. Геометриялық бұрыш жағдайында доға шыңында центрленген және бүйірлерімен шектелген. Айналу жағдайында доға айналу центрінде центрленген және кез келген басқа нүктемен және оның кескіні айналу арқылы шектелген.
Тарих және этимология
Сөз бұрыш шыққан Латын сөз angulus, «бұрыш» деген мағынаны білдіреді; туыстық сөздер Грек ἀγκύλος (анкилос), «қисық, қисық» және Ағылшын сөз «тобық «. Екеуі де Протоинді-еуропалық тамыр * анк-, «иілу» немесе «тағзым» деген мағынаны білдіреді.[2]
Евклид жазықтық бұрышын бір-біріне, жазықтықта, бір-біріне сәйкес келетін және бір-біріне қатысты жатпайтын екі түзудің көлбеуі ретінде анықтайды. Сәйкес Проклус, бұрыш не сапа, не шама, не байланыс болуы керек. Бірінші тұжырымдаманы қолданған Эвдем, бұрышты а-дан ауытқу ретінде қарастырған түзу сызық; екіншісі Антиохия Карпасы, оны қиылысатын сызықтар арасындағы аралық немесе кеңістік ретінде қарастырған; Евклид үшінші тұжырымдаманы қабылдады.[3]
Бұрыштарды анықтау
Жылы математикалық өрнектер, оны пайдалану әдеттегідей Грек әріптері (α, β, γ, θ, φ,. . . ) сияқты айнымалылар кейбір бұрыштың өлшемін білдіретін[4] (оның басқа мағынасымен, символымен шатастырмау үшін π әдетте бұл мақсат үшін пайдаланылмайды). Кіші рим әріптері (а, б, c,. . . ) контексіндегі үлкен римдік әріптер сияқты қолданылады көпбұрыштар. Мысалдар үшін осы мақаладағы суреттерді қараңыз.
Геометриялық фигураларда бұрыштарды оларды анықтайтын үш нүктеге бекітілген белгілер арқылы да анықтауға болады. Мысалы, А және АС сәулелерімен қоршалған А төбесіндегі бұрыш (яғни А нүктесінен В нүктесіне және А нүктесінен С нүктесіне дейінгі түзулер) ∠BAC деп белгіленеді (Юникодта U + 2220 ∠ Бұрыш) немесе . Шатасу қаупі жоқ жерде кейде бұрышты тек оның шыңымен айтуға болады (бұл жағдайда «А бұрышы»).
Ықтимал, ∠BAC деп белгіленетін бұрыш төрт бұрыштың кез-келгеніне сілтеме жасай алады: сағат тілінің В-ден C-ге, B-ден C-ге, C-ден B-ге немесе C-ге қарсы. дейін В, онда бұрыш өлшенетін бағыт оның белгісін анықтайды (қараңыз) Оң және теріс бұрыштар ). Алайда көптеген геометриялық жағдайларда контексттен 180 градустан төмен немесе оған тең оң бұрышты білдіретіні анық, бұл жағдайда екіұштылық туындамайды. Әйтпесе, конвенция қабылдануы мүмкін, сондықтан CBAC әрдайым B-ден C-ге қарсы (оң) бұрышты, ал ∠CAB C-ден B-ге қарсы (оң) бұрышты білдіреді.
Бұрыш түрлері
Жеке бұрыштар
Бұрыштың кейбір жалпы терминологиясы бар, олардың өлшемі әрқашан теріс емес (қараңыз) # Позитивті және жағымсыз бұрыштар ):[5][6]
- 0 ° -қа тең немесе бұрылмаған бұрыш нөлдік бұрыш деп аталады.
- Тік бұрыштан кіші (90 ° кем) бұрыштар деп аталады өткір бұрыштар («өткір» «өткір» дегенді білдіреді).
- Тең бұрыш 1/4 бұрылу (90 ° немесе π/2 радиан) а деп аталады тікбұрыш. Тік бұрышты құрайтын екі сызық деп аталады қалыпты, ортогоналды, немесе перпендикуляр.
- Тік бұрыштан үлкен және түзу бұрыштан кіші (90 ° пен 180 ° аралығында) бұрыштар деп аталады доғал бұрыштар («доғал» «доғал» мағынасын береді).
- Тең бұрыш 1/2 бұраңыз (180 ° немесе π радиан) а деп аталады түзу бұрыш.
- Тік бұрыштан үлкен, бірақ 1 бұрылудан аз (180 ° пен 360 ° аралығында) бұрыштар деп аталады рефлекстік бұрыштар.
- 1 бұрылысқа тең бұрыш (360 ° немесе 2)π радиан) а деп аталады толық бұрыш, толық бұрыш, дөңгелек бұрыш немесе а перигон.
- Тік бұрышты емес бұрыштар немесе тік бұрыштың еселігі деп аталады көлбеу бұрыштар.
Атаулар, интервалдар және өлшем бірліктері төмендегі кестеде көрсетілген:


| Аты-жөні | нөл | өткір | тікбұрыш | доғал | Түзу | рефлекс | перигон | |||
| Бірліктер | Аралық | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Бұрылады | 0 | (0, 1/4) | 1/4 | (1/4, 1/2) | 1/2 | (1/2, 1) | 1 | |||
| Радиандар | 0 | (0, 1/2π) | 1/2π | (1/2π, π) | π | (π, 2π) | 2π | |||
| Дәрежелер | 0° | (0, 90)° | 90° | (90, 180)° | 180° | (180, 360)° | 360° | |||
| Гонс | 0ж | (0, 100)ж | 100ж | (100, 200)ж | 200ж | (200, 400)ж | 400ж | |||
Эквиваленттік бұрыш жұптары
- Бірдей өлшемге ие (яғни бірдей шамада) бұрыштар деп аталады тең немесе үйлесімді. Бұрыш оның өлшемімен анықталады және бұрыштың қабырғаларының ұзындығына тәуелді емес (мысалы, барлығы) тік бұрыштар өлшемі бойынша тең).
- Терминал жақтарын бөлетін, бірақ өлшемі бойынша бұрылыстың бүтін санымен ерекшеленетін екі бұрыш деп аталады котерминалды бұрыштар.
- A сілтеме бұрышы - бұл кез-келген бұрыштың тік бұрышты бірнеше рет азайту немесе қосу арқылы анықталған жедел нұсқасы (1/2 бұрылу, 180 ° немесе π нәтижелеріне қарай қажет болғанша, нәтиже шамасы өткір бұрыш болғанға дейін, мәні 0 мен аралығында болады 1/4 бұрылу, 90 ° немесе π/2 радиан. Мысалы, 30 градус бұрыштың тірек бұрышы 30 градусқа, ал 150 градус бұрышқа да 30 градус (180-150) бұрыш жатады. 750 градус бұрыштың тірек бұрышы 30 градусқа (750-720) тең.[7]
Тік және іргелес бұрыш жұптары

Екі түзу нүктемен қиылысқанда төрт бұрыш пайда болады. Бұл бұрыштар бір-біріне қатысты орналасуына қарай аталады.
- Бір-біріне қарама-қарсы орналасқан, «Х» тәрізді пішінді қалыптастыратын екі қиылысқан түзу сызықтар арқылы құрылған жұп бұрыштар деп аталады. тік бұрыштар немесе қарама-қарсы бұрыштар немесе тігінен қарама-қарсы бұрыштар. Олар қысқартылған ретінде vert. опп. .S.[8]
- Тігінен қарама-қарсы бұрыштардың теңдігі деп аталады тік бұрыш теоремасы. Эвдем Родос дәлелдеуді жатқызды Милет Фалес.[9][10] Ұсыныс көрсеткендей, екі тік бұрыштың екеуі де көршілес екі бұрышқа қосымша болғандықтан, тік бұрыштар өлшемі бойынша тең болады. Тарихи нотаға сәйкес[10] Фалес Египетке барғанда, мысырлықтар қиылысқан екі сызықты сызған сайын, олардың тең екендігіне көз жеткізу үшін тік бұрыштарды өлшейтінін байқады. Фалес келесідей жалпы түсініктерді қабылдаған жағдайда, барлық тік бұрыштардың тең екендігін дәлелдеуге болады деген қорытындыға келді:
- Барлық түзу бұрыштар тең.
- Теңге қосылған теңдік тең болады.
- Барлығынан шығарылған теңдіктер тең болады.
- Екі көрші бұрыш түзу түзгенде, олар қосымша болады. Сондықтан, егер бұрыштың өлшемі деп есептесек A тең х, содан кейін бұрыш өлшемі C 180 болар еді - х. Сол сияқты, бұрыштың өлшемі Д. 180 болар еді - х. Екі бұрыш C және бұрыш Д. 180-ге тең шаралар бар - х және сәйкес келеді. Бұрыштан бастап B екі жағынан да қосымша болып табылады C және Д., бұрыш өлшемін анықтау үшін осы бұрыштық өлшемдердің кез-келгенін қолдануға болады B. Екі бұрыштың өлшемін қолдану C немесе бұрыш D, бұрыштың өлшемін табамыз B 180 болуы керек - (180 - х) = 180 − 180 + х = х. Сондықтан, екі бұрыш A және бұрыш B тең өлшемдері бар х және өлшем бойынша тең.
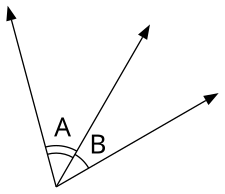
- Іргелес бұрыштар, жиі қысқартылған adj. .S, бұл жалпы төбе мен жиекті бөлісетін, бірақ ішкі нүктелерімен бөліспейтін бұрыштар. Басқаша айтқанда, олар «қолды» бөлісетін немесе көршілес болатын бұрыштар. Тік бұрышты, түзу немесе толық бұрышты қосатын көршілес бұрыштар ерекше, сәйкесінше аталады толықтырушы, қосымша және қосымша бұрыштар (төмендегі «Бұрыш жұптарын біріктіру» бөлімін қараңыз).
A көлденең - бұл (көбіне параллель) жұпты қиып өтетін және байланысты болатын сызық ішкі бұрыштар, сәйкес бұрыштар, ішкі бұрыштар, және сыртқы бұрыштар.[11]
Бұрыш жұптарын біріктіру
Бұрыштардың қосындысын қамтитын үш арнайы бұрыштық жұп бар:

- Қосымша бұрыштар өлшемдері бір тік бұрышқа қосылатын бұрыш жұптары (1/4 бұрылу, 90 ° немесе π/2 радиан).[12] Егер бір-бірін толықтыратын екі бұрыш көрші болса, олардың ортақ емес жақтары тік бұрыш құрайды. Евклидтік геометрияда тік бұрышты үшбұрыштың екі сүйір бұрышы бірін-бірі толықтырады, өйткені а-ның ішкі бұрыштарының қосындысы үшбұрыш 180 градус, ал тік бұрыштың өзі 90 градусқа тең.
- Сын есім латын тілінен алынған қосымша, етістікпен байланысты комплерлер, «толтыру». Тік бұрышты түзу үшін сүйір бұрыш оның толықтырғышымен «толтырылады».
- Бұрыш пен тік бұрыштың айырмашылығы деп аталады толықтыру бұрыштың.[13]
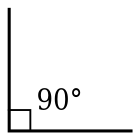
- Егер бұрыштар болса A және B бірін-бірі толықтырады, келесі қатынастар болады:
- (The тангенс бұрыштың теңдеуіне тең котангенс оның толықтауышы мен секанты тең косекант оны толықтырады.)
- The префикс "бірге «кейбір тригонометриялық қатынастардың атауларында» қосымша «сөзіне сілтеме жасалады.
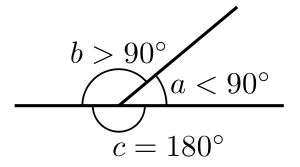
- Тік бұрышты қосатын екі бұрыш (1/2 бұрылу, 180 ° немесе π радиан) деп аталады қосымша бұрыштар.[14]
- Егер екі қосымша бұрыш болса іргелес (яғни жалпыға ортақ шың және тек бір жағын бөлісіңіз), олардың ортақ емес жағы a құрайды түзу сызық. Мұндай бұрыштар а деп аталады сызықтық жұп бұрыштар.[15] Алайда, қосымша бұрыштар бір сызықта болуы шарт емес, оларды кеңістікте бөлуге болады. Мысалы, а-ның іргелес бұрыштары параллелограмм а-ның қосымша және қарама-қарсы бұрыштары болып табылады циклдік төртбұрыш (оның төбелері бір шеңберге түсетін) қосымша болып табылады.
- Егер Р нүктесі O центрі бар шеңбердің сыртында болса және егер жанама сызықтар P-ден T және Q нүктелеріндегі шеңберді түртіңіз, сонда ∠TPQ және ∠TOQ қосымша болады.
- Қосымша бұрыштардың синустары тең. Олардың косинустары мен тангенстері (егер анықталмаған болса) шамасы бойынша тең, бірақ қарама-қарсы белгілері бар.
- Евклидтік геометрияда үшбұрыштағы кез-келген екі бұрыштың қосындысы үшіншісіне қосымша болады, өйткені үшбұрыштың ішкі бұрыштарының қосындысы түзу бұрыш болып табылады.

- Толық бұрышқа қосылатын екі бұрыш (1 бұрылыс, 360 ° немесе 2)π радиан) деп аталады қосымша бұрыштар немесе конъюгаталық бұрыштар.
- Бұрыш пен толық бұрыштың айырмашылығы деп аталады қосымша бұрышының немесе конъюгат бұрыштың.
Көпбұрышқа байланысты бұрыштар

- А-ға кіретін бұрыш қарапайым көпбұрыш деп аталады ішкі бұрыш егер ол сол қарапайым көпбұрыштың ішкі жағында жатса. Қарапайым ойыс көпбұрыш рефлекторлық бұрыш болатын кем дегенде бір ішкі бұрышы бар.
- Жылы Евклидтік геометрия, а ішкі бұрыштарының өлшемдері үшбұрыш қосу π радиан, 180 ° немесе 1/2 бұрылыс; қарапайымның ішкі бұрыштарының өлшемдері дөңес төртбұрышты 2-ге дейін қосыңызπ радиан, 360 ° немесе 1 айналым. Жалпы, қарапайым дөңестің ішкі бұрыштарының өлшемдері көпбұрыш бірге n жақтары (n − 2)π радиан, немесе 180 (n - 2) градус, (2n - 4) тік бұрыштар, немесе (n/2 - 1) бұрылыс.
- Ішкі бұрыштың қосымшасы ан деп аталады сыртқы бұрыш, яғни ішкі бұрыш пен сыртқы бұрыш а құрайды сызықтық жұп бұрыштар. Көпбұрыштың әр төбесінде екі сыртқы бұрыш бар, олардың әрқайсысы төбесінде түйісетін көпбұрыштың екі жағының бірін ұзарту арқылы анықталады; бұл екі бұрыш тік бұрыш, демек, тең. Сыртқы бұрыш көпбұрышты анықтау үшін шыңында айналу керек болатын шаманы өлшейді.[16] Егер сәйкес ішкі бұрыш рефлекторлы бұрыш болса, онда сыртқы бұрышты қарастырған жөн теріс. Қарапайым емес көпбұрыштың өзінде сыртқы бұрышты анықтауға болады, бірақ біреуін таңдау керек болады бағдар туралы ұшақ (немесе беті ) сыртқы бұрыш өлшемінің белгісін шешу.
- Евклидтік геометрияда қарапайым дөңес көпбұрыштың сыртқы бұрыштарының қосындысы бір толық бұрылыс болады (360 °). Мұндағы сыртқы бұрышты а деп атауға болады қосымша сыртқы бұрыш. Сыртқы бұрыштар әдетте қолданылады Тасбақа бағдарламалары тұрақты көпбұрыштарды салу кезінде.
- Ішінде үшбұрыш, биссекторлар екі сыртқы бұрыштың және екінші ішкі бұрыштың биссектрисасы болып табылады қатарлас (бір жерде кездесу).[17]:б. 149
- Үшбұрышта үш қиылысу нүктесі, әрқайсысы қарама-қарсы сыртқы бұрыштың биссектрисасы кеңейтілген жағы, болып табылады коллинеарлы.[17]:б. 149
- Үшбұрышта үш қиылысу нүктесі, олардың екеуі ішкі бұрыш биссектрисасы мен қарама-қарсы жақ арасында, ал үшіншісі басқа сыртқы бұрыш биссектрисасы мен қарама-қарсы бүйір кеңейтілген арасында коллинеар болады.[17]:б. 149
- Кейбір авторлар бұл атауды қолданады сыртқы бұрыш жай мағынасын білдіретін қарапайым көпбұрыштың сыртқы бұрышты орындау (емес қосымша бұрыш!) ішкі бұрышының.[18] Бұл жоғарыда көрсетілгенге қайшы келеді.
Ұшаққа қатысты бұрыштар
- Екі арасындағы бұрыш ұшақтар (мысалы, а-ның екі іргелес беті) полиэдр ) а деп аталады екі жақты бұрыш.[13] Ол екі сызық арасындағы сүйір бұрыш ретінде анықталуы мүмкін қалыпты ұшақтарға.
- Жазықтық пен қиылысатын түзудің арасындағы бұрыш тоқсан градусқа, қиылысатын түзу мен қиылысу нүктесінен өтетін және жазықтыққа қалыпты болатын түзудің арасындағы бұрышты алып тастайды.
Бұрыштарды өлшеу
Бұл туралы айтылды Бұрыштық бірлік болуы біріктірілген осы мақалада. (Талқылаңыз) 2020 жылдың мамыр айынан бастап ұсынылған. |
Геометриялық бұрыштың мөлшері әдетте сәулелердің бірін екіншісіне бейнелейтін ең кіші айналу шамасымен сипатталады. Көлемі бірдей бұрыштар деп аталады тең немесе үйлесімді немесе өлшемі бойынша тең.
Кейбір контексттерде, мысалы, шеңбердегі нүктені анықтау немесе бағдар объектінің анықтамалық бағытқа қатысты екі өлшемді, толықтығының дәл еселігімен ерекшеленетін бұрыштары бұрылу тиімді балама болып табылады. Басқа жағдайда, мысалы, а нүктесін анықтау спираль қисық немесе сипаттайтын кумулятивті айналу объектінің анықтамалық бағытқа қатысты екі өлшемділігі, толық бұрылыстың нөлдік еселігімен ерекшеленетін бұрыштар эквивалентті емес.

Бұрышты өлшеу үшін θ, а дөңгелек доға бұрыштың центріне центрленген, мысалы. жұппен компастар. Ұзындықтың қатынасы с доғаның радиусы бойынша р шеңбердің - бұл бұрыштың өлшемі радиан.
Бұрыштың басқа бұрыштық бірліктегі өлшемі содан кейін оның радиандағы өлшемін масштабтау коэффициентіне көбейту арқылы алынады к/2π, қайда к таңдалған бірліктегі толық айналым өлшемі (мысалы, 360 үшін градус немесе 400 үшін градиандар ):
Мәні θ осылайша анықталған шеңбердің өлшеміне тәуелді емес: егер радиус ұзындығы өзгертілсе, доғаның ұзындығы бірдей пропорцияда өзгереді, сондықтан қатынас с/р өзгертілмеген. (Дәлел. Жоғарыдағы формуланы келесідей етіп жазуға болады к = .r/с. Бір бұрылыс, ол үшін θ = n бірліктер, шеңбердің ұзындығына тең доғаға сәйкес келеді айналдыра, бұл 2πр, сондықтан с = 2πр. Ауыстыру n үшін θ және 2πр үшін с формулада нәтиже шығады к = nr/2πр = n/2π.) [nb 1]
Бұрышты қосу постулаты
Бұрыш қосу постулаты егер болса B бұрыштың ішкі бөлігінде орналасқан AOC, содан кейін
Бұрыштың өлшемі AOC бұл AOB бұрышының және бұрыштың өлшемінің қосындысы BOC. Бұл постулатта қайсысында маңызды емес бірлік әр бұрыш бірдей бірлікте өлшенгенше бұрыш өлшенеді.
Бірліктер
Бұрыштарды бейнелеуге арналған бірліктер төмендеу шамасы бойынша төменде келтірілген. Осы бірліктердің ішінен дәрежесі және радиан ең көп қолданылатындар. Радианмен көрсетілген бұрыштар мақсаттар үшін өлшемсіз өлшемді талдау.
Бұрыштық өлшем бірліктерінің көпшілігі дәл осылай анықталған бұрылу (яғни бір толық шеңбер) тең n бірліктер, кейбір бүтін сан үшін n. Екі ерекшелік - радиан және диаметр бөлігі.
- Бұрылу (n = 1)
- The бұрылу, сонымен қатар цикл, толық шеңбер, революция, және айналу, бұл шеңбер немесе эллипспен толық шеңберлік қозғалыс немесе өлшем (сол нүктеге оралғанда). Кезек қысқартылады τ, цикл, айн, немесе шірік қосымшасына байланысты, бірақ аббревиатурада айн / мин (минутына революция), жай р қолданылады. A бұрылу туралы n қондырғылар арқылы алынады к = 1/2π жоғарыдағы формулада. 1-дің эквиваленттілігі бұрылу 360 °, 2 құрайдыπ рад, 400 град және 4 тік бұрыш. Таңба τ а ретінде де қолданыла алады математикалық тұрақты 2. көрсетуπ радиан. Осылайша қолданылады (к = τ/2π) радианның бұрылыс бөлшегі түрінде көрінуіне мүмкіндік береді. Мысалы, жарты айналым τ/2 = π.
- Төрттік (n = 4)
- The ширек болып табылады 1/4 бұрылыстың, яғни а тікбұрыш. Бұл қолданылған бірлік Евклидтің элементтері. 1 квадрат. = 90 ° = π/2 рад = 1/4 бұрылыс = 100 град. Неміс тілінде символ ∟ квадрантты белгілеу үшін қолданылған.
- Секстант (n = 6)
- The секстант (бұрышы тең бүйірлі үшбұрыш ) болып табылады 1/6 кезек. Бұл қолданылған қондырғы болды Вавилондықтар,[20][21] және сызғыш пен циркульмен салу оңай. Доғаның дәрежесі, минуты және секунды жыныстық аз Вавилон бөлімшесінің бөлімшелері. 1 Вавилондық бірлік = 60 ° = π/ 3 рад ≈ 1.047197551 рад.

- Радиан (n = 2π = 6.283 . . . )
- The радиан - шеңбер радиусымен бірдей ұзындықтағы шеңбер доғасы арқылы түсірілген бұрыш. Ертерек берілген формула үшін радианның жағдайы, а радиан туралы n = 2π қондырғылар арқылы алынады к = 2π/2π = 1. Бір айналым - 2π радиан, ал бір радиан - 180/π градус, немесе шамамен 57.2958 градус. Радиан қысқартылған раддегенмен, бұл таңба математикалық мәтіндерде жиі көрсетілмейді, егер басқаша көрсетілмесе, радиандар қабылданады. Радиандар қолданылған кезде бұрыштар өлшемсіз болып саналады. Радиан қарапайым практикалық геометриядан тыс барлық математикалық жұмыстарда қолданылады, мысалы, жағымды және «табиғи» қасиеттерге байланысты тригонометриялық функциялар олардың аргументтері радиан болғанда көрсету. Радиан дегеніміз - ішіндегі бұрыштық өлшем бірлігі (алынған) SI жүйе.
- Сағат позициясы (n = 12)
- Сағаттың позициясы - салыстырмалы бағыт а-ның ұқсастығын пайдаланып сипатталған объектінің 12 сағаттық сағат. Тік немесе тегіс жатқан сағат тілінің айналасын елестетіп, он екі сағаттық белгілерді бағыттарымен анықтайды.
- Сағат бұрышы (n = 24)
- Астрономиялық сағаттық бұрыш болып табылады 1/24 кезек. Бұл жүйе тәулігіне бір рет айналатын заттарды өлшеуге ыңғайлы болғандықтан (мысалы, жұлдыздардың өзара орналасуы), жыныстық аз суббірліктер деп аталады минуттың уақыты және екінші уақыт. Бұл доғаның минуттарынан және секундтарынан ерекшеленеді, ал 15 есе үлкен. 1 сағат = 15 ° = π/12 рад = 1/6 төрттік. = 1/24 бұрылу = 16+2/3 град.
- (Компас) нүкте немесе жел (n = 32)
- The нүкте, қолданылған навигация, болып табылады 1/32 кезек. 1 ұпай = 1/8 тік бұрыштың = 11,25 ° = 12,5 град. Әр ұпай төрт ширек-ұпайға бөлінеді, осылайша 1 айналым 128 ширек ұпайға тең болады.
- Hexacontade (n = 60)
- The hexacontade 6 ° бірлігі Эратосфен пайдаланылды, осылайша тұтас бір айналым 60 бірлікке бөлінді.
- Пехус (n = 144–180)
- The печус болды Вавилондық шамамен 2 ° немесе 2+1/2°.
- Екілік дәреже (n = 256)
- The екілік дәреже, деп те аталады екілік радиан (немесе брад), болып табылады 1/256 кезек.[22] Екілік дәреже есептеуді бұрышта бір мәнде тиімді түрде көрсетілетіндей етіп қолданылады байт (шектеулі дәлдікке қарамастан). Есептеу кезінде қолданылатын бұрыштың басқа өлшемдері бір бүтін бұрылысты 2-ге бөлуге негізделуі мүмкінn басқа мәндері үшін тең бөліктер n.[23]
- Дәрежесі (n = 360)
- The дәрежесі, кіші жоғарғы сызық шеңберімен (°) белгіленсе, 1/360 айналымға тең, сондықтан бір бұрылу 360 ° құрайды. Ертерек берілген формула үшін дәрежелер жағдайы, а дәрежесі туралы n = 360 ° бірлік орнату арқылы алынады к = 360°/2π. Мұның ескі артықшылығы жыныстық аз суббірлік - қарапайым геометрияда кездесетін көптеген бұрыштар бүтін градус санымен өлшенеді. Дәреженің бөлшектері қалыпты ондық белгімен жазылуы мүмкін (мысалы, үш жарым градус үшін 3,5 °), бірақ «градус-минут-секунд» жүйесінің «минут» және «екінші» сексагимальды суббірліктері де қолданылады, әсіресе үшін географиялық координаттар және астрономия және баллистика.
- Диаметр бөлігі (n = 376.99 . . . )
- The диаметрі (кейде ислам математикасында қолданылады) болып табылады 1/60 радиан. Бір «диаметрлі бөлік» шамамен 0,95493 ° құрайды. Бір айналымда шамамен 376,991 диаметрлі бөлшектер бар.
- Град (n = 400)
- The град, деп те аталады баға, градиан, немесе гон, болып табылады 1/400 бұрылыстың бұрышы, сондықтан тік бұрыш 100 градусты құрайды.[4] Бұл квадранттың ондық суббірлігі. A километр ретінде тарихи анықталды цент -жер доғасы Жердің үлкен шеңбері бойымен, сондықтан километр ондыққа ұқсас ондыққа тең жыныстық аз теңіз милі. Град негізінен қолданылады триангуляция.
- Миллирадиандық
- Миллирадиан (миль немесе мрад) радианның мыңнан бір бөлігі ретінде анықталады, яғни бір айналым бұрылу 2000π мильден (немесе шамамен 6283.185 ... миль), және барлығынан тұрады көрікті жерлер үшін атыс қаруы осы анықтамаға сәйкес калибрленген. Сонымен қатар артиллерия мен навигация үшін қолданылатын тағы үш анықтама бар шамамен миллирадиялыққа тең. Осы үш басқа анықтама бойынша бір айналым дәл 6000, 6300 немесе 6400 мильді құрайды, бұл 0,05625-тен 0,06 градусқа дейін (3,375-тен 3,6 минутқа дейін). Салыстыру үшін, нағыз миллирадиан шамамен 0,05729578 ... градус (3,43775 ... минут) құрайды. Бір »НАТО миль »ретінде анықталады 1/6400 шеңбердің. Шынайы миллирадия сияқты, басқа да анықтамалардың әрқайсысы мильдің қосалқы күшінің қасиетін пайдаланады, яғни бір миллирадтың мәні 1 км алшақтықтан көрінгендей, ені 1 метрдің бұрышына тең болады (2π/6400 = 0.0009817... ≈ 1/1000).
- Доға минуты (n = 21,600)
- The доға минуты (немесе MOA, аркминут, немесе жай минут) болып табылады 1/60 дәреже = 1/21,600 бұрылу. Ол бір қарапайым (′) арқылы белгіленеді. Мысалы, 3 ° 30 ′ 3 × 60 + 30 = 210 минутқа немесе 3 + -ге тең30/60 = 3,5 градус. Кейде ондық бөлшектермен аралас формат қолданылады, мысалы. 3 ° 5.72 ′ = 3 +5.72/60 градус. A теңіз милі тарихи а. бойымен доға минуты ретінде анықталды үлкен шеңбер Жердің
- Доғаның секунды (n = 1,296,000)
- The доғаның екінші бөлігі (немесе доғалық секунд, немесе жай екінші) болып табылады 1/60 доға минутының және 1/3600 дәреже Ол екі еселенген жай (″) арқылы белгіленеді. Мысалы, 3 ° 7 ′ 30 ″ 3 + -ге тең 7/60 + 30/3600 градус немесе 3,125 градус.
- Миллиарксекунд (n = 1,296,000,000)
- мас
- Микроарсекунд (n = 1,296,000,000,000)
- солай
Оң және теріс бұрыштар
Бұрыш өлшеуінің анықтамасы теріс бұрыш ұғымын қолдамаса да, оң және теріс бұрыштық мәндерді көрсетуге мүмкіндік беретін конвенцияны қолдану пайдалы. бағдарлар және / немесе айналу кейбір сілтемелерге қатысты қарама-қарсы бағытта.
Екі өлшемді Декарттық координаттар жүйесі, бұрыш әдетте оның екі жағымен анықталады, оның шыңы басында. The бастапқы жағы оң жағында х осі, ал екінші жағы немесе терминал жағы бастапқы жағынан радианмен, градуспен немесе бұрылыспен өлшеу арқылы анықталады. Бірге оң бұрыштар оңға қарай айналуды бейнелейді у осі және теріс бұрыштар теріске қарай бұрылыстарды бейнелейді ж-аксис. Декарттық координаталар ұсынылған кезде стандартты позиция, арқылы анықталады х- оңға бағытталған және ж- оңға айналу, оң айналу сағат тіліне қарсы және теріс айналулар болып табылады сағат тілімен.
Көптеген жағдайда бұрышы -θ «минус бір толық бұрылыс» бұрышына тиімді θ«. Мысалы, -45 ° түрінде көрсетілген бағдар 360 ° - 45 ° немесе 315 ° түрінде көрсетілген бағдармен тиімді түрде тең. Соңғы позиция бірдей болғанымен, a45 ° физикалық айналу (қозғалыс) 315 ° бұрылумен бірдей (мысалы, шаңды еденге сүйеніп тұрған сыпырғышты ұстап тұрған адамның айналуы еденде сыпырылған аймақтардың көзбен әр түрлі іздерін қалдырады).
Үш өлшемді геометрияда «сағат тілімен» және «сағат тіліне қарсы» абсолютті мағына жоқ, сондықтан оң және теріс бұрыштардың бағыты кейбір сілтемелерге қатысты анықталуы керек, бұл әдетте вектор бұрыштың төбесі арқылы және бұрыштың сәулелері жатқан жазықтыққа перпендикуляр.
Жылы навигация, мойынтіректер немесе азимут солтүстікке қатысты өлшенеді. Шарт бойынша, жоғарыдан қараған кезде тіреу бұрыштары сағат тілінің оң жағына ие, сондықтан 45 ° тіреу солтүстік-шығыс бағытына сәйкес келеді. Теріс мойынтіректер навигацияда пайдаланылмайды, сондықтан солтүстік-батыс бағыт 315 ° мойынтіректеріне сәйкес келеді.
Бұрыш өлшемін өлшеудің баламалы тәсілдері
Бұрыштың өлшемін айналу бұрышымен өлшеудің бірнеше баламасы бар.The көлбеудің деңгейі, немесе градиент тең тангенс бұрышының немесе кейде (сирек) синус. Градиент көбінесе пайызбен көрсетіледі. Өте аз мәндер үшін (5% -дан аз) көлбеудің деңгейі шамамен радиандағы бұрыштың өлшемі болып табылады.
Жылы рационалды геометрия The таратамын екі түзудің арасындағы түзулер арасындағы бұрыштың синусының квадраты ретінде анықталады. Бұрыштың синусы мен оның қосымша бұрышының синусы бірдей болғандықтан, түзулердің бірін екіншісіне бейнелейтін кез келген айналу бұрышы түзулер арасындағы таралу үшін бірдей мәнге әкеледі.
Астрономиялық жуықтамалар
Астрономдар объектілердің бұрыштық бөлінуін олардың бақылау нүктелерінен градуспен өлшейді.
- 0,5 ° - бұл күннің немесе айдың ені.
- 1 ° - бұл саусақтың қол ұзындығындағы ені.
- 10 ° - бұл қолдың ұзындығындағы жабық жұдырықтың ені.
- 20 ° - бұл қолдың ұзындығындағы алақанның ені.
Бұл өлшемдер жеке зерттелушіге байланысты, ал жоғарыдағылар өрескел деп саналуы керек бас бармақ ережесі тек жуықтау.
Қисықтар арасындағы бұрыштар

Түзу мен а арасындағы бұрыш қисық (аралас бұрыш) немесе екі қиылысатын қисықтар арасындағы (қисық сызықты бұрыш) - арасындағы бұрыш ретінде анықталады тангенстер қиылысу нүктесінде. Белгілі бір жағдайларға әртүрлі атаулар берілді (қазір сирек, тіпті сирек қолданылады):амфикиртикалық (Гр. ἀμφί, екі жағында, κυρτός, дөңес) немесе циссоидты (Гр. Κισσός, шырмауық), қос дөңес; Xistroidal немесе систроидальды (Гр. Ξυστρίς, қыруға арналған құрал), конкаво-дөңес; амфикоэл (Гр. Κοίλη, қуыс) немесе angulus lunularis, биконкав.[24]
Бұрыштарды екіге бөлу және үштікке бөлу
The ежелгі грек математиктері а-ны пайдаланып, бұрышты екіге бөлуді (оны бірдей өлшемнің екі бұрышына бөлуді) білді циркуль және түзу, бірақ белгілі бір бұрыштарды тек үшке бөлуге болатын. 1837 жылы Пьер Вантцель көптеген бұрыштар үшін бұл құрылысты жүзеге асыруға болмайтынын көрсетті.
Нүктелік өнім және жалпылау
Ішінде Евклид кеңістігі, бұрыш θ екеуінің арасында Евклидтік векторлар сен және v олармен байланысты нүктелік өнім және олардың ұзындығы формула бойынша
Бұл формула екі жазықтықтың (немесе қисық беттің) олардың арасындағы бұрышты табу әдісін ұсынады қалыпты векторлар және арасында қисық сызықтар олардың векторлық теңдеулерінен.
Ішкі өнім
Бұрыштарды дерексіз шындықта анықтау ішкі өнім кеңістігі, біз эвклидтік нүктелік өнімді ауыстырамыз ( · ) ішкі өніммен , яғни
Кешенде ішкі өнім кеңістігі, жоғарыдағы косинустың өрнегі нақты емес мәндерді бере алады, сондықтан ол ауыстырылады
немесе, көбінесе, абсолютті мәнді қолдана отырып
Соңғы анықтама векторлардың бағытын ескермейді және осылайша бір өлшемді ішкі кеңістіктер арасындағы бұрышты сипаттайды және векторлармен және сәйкесінше.
Ішкі кеңістіктер арасындағы бұрыштар
Бір өлшемді ішкі кеңістіктер арасындағы бұрыштың анықтамасы және берілген
ішінде Гильберт кеңістігі кез келген ақырлы өлшемді ішкі кеңістіктерге дейін кеңейтілуі мүмкін. Екі кіші кеңістік берілген , бірге , бұл анықтамаға әкеледі канондық немесе деп аталатын бұрыштар негізгі бұрыштар ішкі кеңістіктер арасында.
Риман геометриясындағы бұрыштар
Жылы Риман геометриясы, метрикалық тензор екеуінің арасындағы бұрышты анықтау үшін қолданылады тангенстер. Қайда U және V жанама векторлар болып табылады жиж метрикалық тензордың компоненттері болып табылады G,
Гиперболалық бұрыш
A гиперболалық бұрыш болып табылады дәлел а гиперболалық функция сияқты дөңгелек бұрыш а аргументі дөңгелек функция. Салыстыруды а саңылауларының өлшемі ретінде көруге болады гиперболалық сектор және а дөңгелек сектор бастап аудандар осы секторлардың әрқайсысының бұрыш шамаларына сәйкес келеді. Дөңгелек бұрыштан айырмашылығы, гиперболалық бұрыш шексіз. Дөңгелек және гиперболалық функциялар ретінде қарастырылғанда шексіз серия олардың бұрыштық аргументінде дөңгелек әділ айнымалы қатарлар гиперболалық функциялардың формалары. Бұрыш пен функцияның екі түрін осылай тоқу түсіндірілді Леонхард Эйлер жылы Шексіз талдауға кіріспе.
География мен астрономиядағы бұрыштар
Жылы география, Жердегі кез-келген нүктенің орнын a көмегімен анықтауға болады географиялық координаттар жүйесі. Бұл жүйе ендік және бойлық көмегімен кез-келген орналасу жердің центрінде орналасқан бұрыштар бойынша экватор және (әдетте) Гринвич меридианы сілтемелер ретінде
Жылы астрономия, берілген нүкте аспан сферасы (яғни астрономиялық объектінің айқын орналасуы) кез-келгенінің кез-келгенін пайдаланып анықталуы мүмкін координаттардың астрономиялық жүйелері, онда сілтемелер белгілі бір жүйеге сәйкес өзгеріп отырады. Астрономдар өлшейді бұрыштық бөлу екеуінің жұлдыздар центрі арқылы екі жолды елестету арқылы Жер, әрқайсысы жұлдыздардың бірін қиып өтеді. Сол сызықтар арасындағы бұрышты өлшеуге болады және бұл екі жұлдыз арасындағы бұрыштық бөліну.
Географияда да, астрономияда да а бағытымен анықтауға болады тік бұрыш сияқты биіктік /биіктік қатысты көкжиек сияқты азимут құрметпен солтүстік.
Астрономдар сонымен бірге өлшейді айқын өлшем нысандар ретінде бұрыштық диаметр. Мысалы, толған ай Жерден қарағанда бұрыштық диаметрі шамамен 0,5 °. «Айдың диаметрі жарты градус бұрыш жасайды» деп айтуға болады. The кіші бұрыш формуласы осындай бұрыштық өлшеуді арақашықтық / өлшем қатынасына айналдыру үшін қолдануға болады.
Сондай-ақ қараңыз
- Бұрыш биссектрисасы
- Бұрыштық жылдамдық
- Аргумент (кешенді талдау)
- Астрологиялық аспект
- Орталық бұрыш
- Сағат бұрышы мәселесі
- Екі жақты бұрыш
- Сыртқы бұрыш теоремасы
- Алтын бұрыш
- Шеңбердің үлкен қашықтығы
- Жазылған бұрыш
- Иррационалды бұрыш
- Фаза (толқындар)
- Өткізгіш
- Қатты бұрыш үш өлшемдегі бұрыш ұғымы үшін.
- Сфералық бұрыш
- Трансценденттік бұрыш
- Трисекция
- Зенит бұрышы
Ескертулер
- ^ Бұл тәсіл бұрыштың радиусы өзгерген сайын өзгермейтіндігіне қосымша дәлелдеуді қажет етеді р, «таңдалған өлшем бірліктері» мәселесіне қосымша. Тегіс тәсіл - бұрышты сәйкес бірлік шеңбер доғасының ұзындығымен өлшеу. Мұнда «бірлік» өлшем сызғыш ретінде таңдалуы мүмкін, өйткені ол нақты сызықтағы бірлік сегментімен байланысты нақты 1 саны. Мысалы, Радослав М.Димитричті қараңыз.[19]
Әдебиеттер тізімі
- ^ Сидоров 2001 ж
- ^ Slocum 2007
- ^ Чишолм 1911; Хайберг 1908 ж, 177–178 бб
- ^ а б «Математикалық рәміздер жинағы». Математикалық қойма. 2020-03-01. Алынған 2020-08-17.
- ^ «Бұрыштар - өткір, доғал, түзу және дұрыс». www.mathsisfun.com. Алынған 2020-08-17.
- ^ Вайсштейн, Эрик В. «Бұрыш». mathworld.wolfram.com. Алынған 2020-08-17.
- ^ «Математикалық сөздер: сілтеме бұрышы». www.mathwords.com. Мұрағатталды түпнұсқадан 2017 жылғы 23 қазанда. Алынған 26 сәуір 2018.
- ^ Wong & Wong 2009 ж, 161–163 бб
- ^ Евклид. Элементтер. I ұсыныс: 13.
- ^ а б Shute, Shirk & Porter 1960 ж, 25-27 б.
- ^ Джейкобс 1974 ж, б. 255.
- ^ «Қосымша бұрыштар». www.mathsisfun.com. Алынған 2020-08-17.
- ^ а б Чишолм 1911
- ^ «Қосымша бұрыштар». www.mathsisfun.com. Алынған 2020-08-17.
- ^ Джейкобс 1974 ж, б. 97.
- ^ Хендерсон және Таймина 2005 ж, б. 104.
- ^ а б c Джонсон, Роджер А. Жетілдірілген эвклидтік геометрия, Dover Publications, 2007 ж.
- ^ Д. Цвиллингер, ред. (1995), CRC Standard Mathematical Tables and Formulae, Boca Raton, FL: CRC Press, p. 270 as cited in Вайсштейн, Эрик В. "Exterior Angle". MathWorld.
- ^ Dimitrić, Radoslav M. (2012). "On Angles and Angle Measurements" (PDF). The Teaching of Mathematics. XV (2): 133–140. Мұрағатталды (PDF) from the original on 2019-01-17. Алынған 2019-08-06.
- ^ Jeans, James Hopwood (1947). The Growth of Physical Science. CUP мұрағаты. б.7.
- ^ Murnaghan, Francis Dominic (1946). Analytic Geometry. б. 2018-04-21 121 2.
- ^ "ooPIC Programmer's Guide - Chapter 15: URCP". ooPIC Manual & Technical Specifications - ooPIC Compiler Ver 6.0. Savage Innovations, LLC. 2007 [1997]. Архивтелген түпнұсқа on 2008-06-28. Алынған 2019-08-05.
- ^ Hargreaves, Shawn. "Angles, integers, and modulo arithmetic". blogs.msdn.com. Мұрағатталды from the original on 2019-06-30. Алынған 2019-08-05.
- ^ Чишолм 1911; Heiberg 1908, б. 178
Библиография
- Henderson, David W.; Taimina, Daina (2005), Experiencing Geometry / Euclidean and Non-Euclidean with History (3rd ed.), Pearson Prentice Hall, p. 104, ISBN 978-0-13-143748-7
- Heiberg, Johan Ludvig (1908), Heath, T. L. (ed.), Евклид, The Thirteen Books of Euclid's Elements, 1, Кембридж: Cambridge University Press.
- Sidorov, L. A. (2001) [1994], "Angle", Математика энциклопедиясы, EMS Press
- Jacobs, Harold R. (1974), Геометрия, W. H. Freeman, pp. 97, 255, ISBN 978-0-7167-0456-0
- Slocum, Jonathan (2007), Preliminary Indo-European lexicon — Pokorny PIE data, University of Texas research department: linguistics research center, алынды 2 Feb 2010
- Shute, William G.; Shirk, William W.; Porter, George F. (1960), Plane and Solid Geometry, American Book Company, pp. 25–27
- Wong, Tak-wah; Wong, Ming-sim (2009), "Angles in Intersecting and Parallel Lines", New Century Mathematics, 1В (1 ed.), Hong Kong: Oxford University Press, pp. 161–163, ISBN 978-0-19-800177-5
![]() This article incorporates text from a publication now in the қоғамдық домен: Чисхольм, Хью, ред. (1911), "Бұрыш ", Britannica энциклопедиясы, 2 (11th ed.), Cambridge University Press, p. 14
This article incorporates text from a publication now in the қоғамдық домен: Чисхольм, Хью, ред. (1911), "Бұрыш ", Britannica энциклопедиясы, 2 (11th ed.), Cambridge University Press, p. 14
Сыртқы сілтемелер
- , Britannica энциклопедиясы, 2 (9th ed.), 1878, pp. 29–30
- Proximity construction of an angle in decimal degrees with the third intercept theorem
- Angle Bisectors in a Quadrilateral кезінде cut-the-knot
- Constructing a triangle from its angle bisectors кезінде cut-the-knot
- Various angle constructions with compass and straightedge
- Complementary Angles animated demonstration. With interactive applet
- Supplementary Angles animated demonstration. With interactive applet
- Angle definition pages with interactive applets that are also useful in a classroom setting. Math Open Reference
- Construction of an angle[тұрақты өлі сілтеме ] Site geometry


![{displaystyle { egin{aligned}&sin ^{2}A+sin ^{2}B=1&&cos ^{2}A+cos ^{2}B=1[3pt]& an A=cot B&&sec A=csc Bend{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/47aa6b35b8e53468f73d7ec051d55371da314fba)
















